
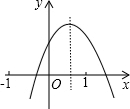
 拋物線y=ax2+bx+c圖象如圖,有下列7個結論:
拋物線y=ax2+bx+c圖象如圖,有下列7個結論:| A. | 3個 | B. | 4個 | C. | 5個 | D. | 6個 |
分析 由拋物線的開口方向判斷a與0的關系,由拋物線與y軸的交點判斷c與0的關系,然后根據對稱軸及拋物線與x軸交點情況進行推理,進而對所得結論進行判斷.
解答 解:①∵拋物線的開口方向向下,
∴a<0,
∵拋物線與y軸的交點為在y軸的正半軸上,
∴c>0,
∵拋物線對稱軸在y軸右側,
∴對稱軸x=-$\frac{b}{2a}$>0,
∴b>0,
故abc<0;
故本選項錯誤;
②根據拋物線在x=-1時,y<0,即y=a×(-1)2+b(-1)+c=a-b+c<0
∴a+c<b,故選項錯誤.
③根據圖示知,當x=2時,y<0,即4a+2b+c<0;
故本選項錯誤;
④根據拋物線在x=-1時,y<0,即y=a-b+c<0,
∵0<-$\frac{b}{2a}$<1,
∴a<-$\frac{b}{2}$,
∴不能確定-$\frac{b}{2}$-b+c<0,
∴不能確定2c<3b,
故本選項錯誤;
⑤由圖可知 當 x=-1 時,y=a-b+c<0,
∴a+c<b>0,即不確定a+c>0;
故本選項錯誤;
⑥根據圖示知,當-$\frac{b}{2a}$<m<1時,a+b>m(am+b)(m≠1)不成立;
故本選項錯誤;
⑦根據圖示知,當x=-3時,y<0,即9a-3b+c<0;
故本選項正確;
綜上所述,只有1個正確.
故選D.
點評 本題主要考查圖象與二次函數系數之間的關系,重點是從圖象中找出重要信息;注意掌握數形結合思想的應用.


 口算題卡加應用題集訓系列答案
口算題卡加應用題集訓系列答案科目:初中數學 來源: 題型:選擇題
| A. | $\frac{\sqrt{y}}{x}$ | B. | $\frac{\sqrt{-y}}{x}$ | C. | $\frac{-\sqrt{y}}{x}$ | D. | $\frac{-\sqrt{-y}}{x}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
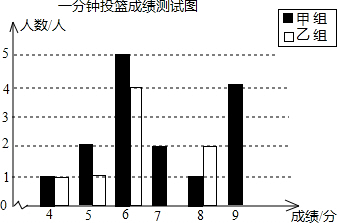
| 成績(分) | 4 | 5 | 6 | 7 | 8 | 9 |
| 甲組(人) | 1 | 2 | 5 | 2 | 1 | 4 |
| 乙組(人) | 1 | 1 | 4 | 5 | 2 | 2 |
| 統計量 | 平均分 | 方差 | 中位數 | 合格率 | 優秀率 |
| 甲組 | 6.8 | 2.56 | 6 | 80.0% | 26.7% |
| 乙組 | 6.8 | 1.76 | 7 | 86.7% | 13.3% |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 941×108 | B. | 94.1×109 | C. | 9.41×1010 | D. | 9.41×1011 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
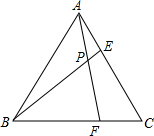 等邊三角形ABC的邊長為6,在AC,BC邊上各取一點E,F,連接AF,BE相交于點P;
等邊三角形ABC的邊長為6,在AC,BC邊上各取一點E,F,連接AF,BE相交于點P;查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com