
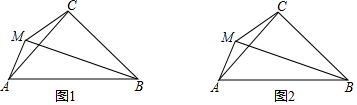
分析 (1)如圖1,根據CM平分∠AMB的外角,得∠CMB=45°,由∠AMB=∠ACB=90°,知A、M、C、B四點共圓,則∠CAB=∠CMB=45°,得△ACB是等腰直角三角形,則CA=CB;
(2)解法一:作輔助線,構建四邊形HMGC,證明四邊形HMGC是正方形,得:HM=CG=CH=MG,再證明△ACH≌△BCG(SAS),則BG=AH,表示BM-AM的差,并用相等的線段代換可得結論;
解法二:如圖3,作輔助線,構建全等三角形,證明△ADC≌△BMC,得DC=MC,∠ACD=∠BCM,
從而得△DCM是等腰直角三角形,所以DM=$\sqrt{2}$CM,代入BM-AM=AD-AM可得結論.
解答 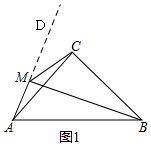 證明:(1)如圖1,延長AM至D,
證明:(1)如圖1,延長AM至D,
∵AM⊥BM,
∴∠BMD=90°,
∵CM平分∠BMD,
∴∠CMB=$\frac{1}{2}$∠BMD=$\frac{1}{2}$×90°=45°,
∵∠AMB=∠ACB=90°,
∴A、M、C、B四點共圓,
∴∠CAB=∠CMB=45°,
∴△ACB是等腰直角三角形,
∴CA=CB;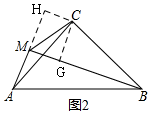
(2)解法一:如圖2,過C作CH⊥AM,交AM的延長線于H,過C作CG⊥BM于G,
∵∠H=∠HMG=∠MGC=90°,
∴四邊形HMGC是矩形,
∵∠CMB=45°,
∴△MGC是等腰直角三角形,
∴MG=CG,
∴矩形HMGC是正方形,
∴HM=CG=CH=MG,
∵∠ACH+∠ACG=90°,
∠BCG+∠ACG=90°,
∴∠ACH=∠BCG,
在△ACH和△BCG中,
∵$\left\{\begin{array}{l}{CH=CG}\\{∠ACH=∠BCG}\\{AC=BC}\end{array}\right.$,
∴△ACH≌△BCG(SAS),
∴BG=AH,
在Rt△MCH中,∠CMH=45°,
∴CM=$\sqrt{2}$MH,即$\sqrt{2}$CM=2MH,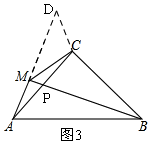
∵BM-AM=BG+MG-AM=AH+MG-AM=AM+MH+MG-AM=2MH,
∴BM-AM=$\sqrt{2}$CM;
解法二:如圖3,延長AM至D,使AD=BM,連接CD,
∵∠AMB=∠ACB=90°,∠APM=∠BPC,
∴∠DAC=∠MBC,
在△ADC和△BMC中,
∵$\left\{\begin{array}{l}{AD=BM}\\{∠DAC=∠MBC}\\{AC=BC}\end{array}\right.$,
∴△ADC≌△BMC(SAS),
∴DC=MC,∠ACD=∠BCM,
∴∠ACD-∠ACM=∠BCM-∠ACM,
即∠ACB=∠MCD=90°,
∴△DCM是等腰直角三角形,
∴DM=$\sqrt{2}$CM,
∵BM-AM=AD-AM=AM+DM-AM=DM=$\sqrt{2}$CM.
點評 本題考查了三角形全等的性質和判定、等腰直角三角形的性質和判定、四點共圓的性質和判定,本題作輔助線,構建全等三角形是關鍵,利用三角形全等的性質:對應邊相等將線段的差進行轉化,并與等腰直角三角形斜邊是直角邊的$\sqrt{2}$倍相結合,使問題得以解決.


 期末沖刺100分創新金卷完全試卷系列答案
期末沖刺100分創新金卷完全試卷系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
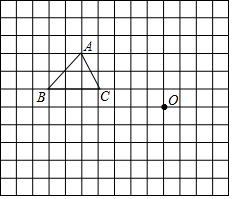 如圖,△ABC是格點三角形,按下列要求作圖:
如圖,△ABC是格點三角形,按下列要求作圖:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
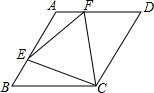 如圖,菱形ABCD中,∠B=60°,AB=2,點E、F分別是AB、AD上的動點,且滿足BE=AF,接連EF、EC、CF.求證:△EFC是等邊三角形.
如圖,菱形ABCD中,∠B=60°,AB=2,點E、F分別是AB、AD上的動點,且滿足BE=AF,接連EF、EC、CF.求證:△EFC是等邊三角形.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
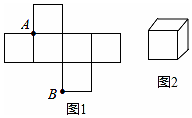 如圖1是邊長為1的六個小正方形組成的平面圖形,將它圍成圖2的正方體,則圖1中小正方形頂點A,B在圍成的正方體上的距離是( )
如圖1是邊長為1的六個小正方形組成的平面圖形,將它圍成圖2的正方體,則圖1中小正方形頂點A,B在圍成的正方體上的距離是( )| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | 1 | D. | 0 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com