
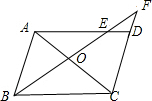
 如圖,平行四邊形ABCD中,過B點作直線交AC、AD于O、E,交CD的延長線于F點,
如圖,平行四邊形ABCD中,過B點作直線交AC、AD于O、E,交CD的延長線于F點,分析 (1)由AB∥CD得到△AOB∽△COE,于是得到OE:OB=OC:OA,根據AD∥BC于是得到△AOF∽△COB,推出OB:OF=OC:OA,進而得出OB2=OF•OE;
(2)由平行四邊形的性質:對邊平行易證△ABE∽△DFE,再由相似三角形的性質:對應邊的比值相等即可求出AE的長.
解答 解:
(1)證明:∵四邊形ABCD是平行四邊形,
∴AB∥CD,
∴△AOB∽△COE.
∴OE:OB=OC:OA;
∵AD∥BC,
∴△AOF∽△COB.
∴OB:OF=OC:OA.
∴OB:OF=OE:OB,
即OB2=OF•OE;
(2)∵四邊形ABCD是平行四邊形,
∴AB∥CD,AD=BC=6,
∴△ABE∽△DFE,
∴DF:AB=DE:AE,
∵AB=4,DF=2,
∴2:4=(6-AE):AE,
解得:AE=4.
點評 此題考查了相似三角形的判定和性質,綜合性較強,有一定難度,證線段的乘積相等,通常轉化為比例式形式,再證明所在的三角形相似,熟練掌握相似三角形的判定和性質是解題的關鍵.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:填空題
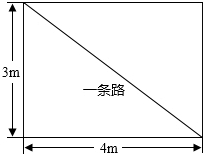 在“尋找濱河最美,拒絕不文明行為”系列活動中,細心的董明同學發現:學校六號樓前有一塊長方形花圃(如圖所示),有極少數人為了避開拐角走“捷徑”,在花圃內走出了一條“路”,請你計算,他們僅僅少走了4步路(假設2步為1米),卻踩傷了花草.
在“尋找濱河最美,拒絕不文明行為”系列活動中,細心的董明同學發現:學校六號樓前有一塊長方形花圃(如圖所示),有極少數人為了避開拐角走“捷徑”,在花圃內走出了一條“路”,請你計算,他們僅僅少走了4步路(假設2步為1米),卻踩傷了花草.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | ①④ | B. | ②④ | C. | ②③ | D. | ①③ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
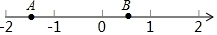 如圖,一只螞蟻從點A沿數軸向右爬了2個單位長度到達點B,點A表示-1$\frac{1}{2}$,設點B所表示的數為m
如圖,一只螞蟻從點A沿數軸向右爬了2個單位長度到達點B,點A表示-1$\frac{1}{2}$,設點B所表示的數為m查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com