

分析 ②梯形的面積可以由梯形的面積公式求出,也可利用三個直角三角形面積求出,兩次求出的面積相等列出關系式,化簡即可得證;
③連結DB,過點D作BC邊上的高DF,則DF=EC=b-a根據S四邊形ADCB=S△ACD+S△ABC,S四邊形ADCB=S△ADB+S△DCB列出關系式,化簡即可得證;
④根據題意,我們可在圖中找等量關系,由中間的小正方形的面積等于大正方形的面積減去四個直角三角形的面積,列出等式化簡即可得出勾股定理的表達式..
解答 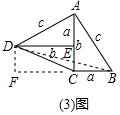 解:②梯形的面積為$\frac{1}{2}$(a+b)(a+b)=$\frac{1}{2}$a2+ab+$\frac{1}{2}$b2,
解:②梯形的面積為$\frac{1}{2}$(a+b)(a+b)=$\frac{1}{2}$a2+ab+$\frac{1}{2}$b2,
也可利用表示為$\frac{1}{2}$ab+$\frac{1}{2}$c2+$\frac{1}{2}$ab,
∴$\frac{1}{2}$a2+ab+$\frac{1}{2}$b2=$\frac{1}{2}$ab+$\frac{1}{2}$c2+$\frac{1}{2}$ab,即a2+b2=c2
②連結DB,過點D作BC邊上的高DF,則DF=EC=b-a
∵S四邊形ADCB=S△ACD+S△ABC=$\frac{1}{2}$b2+$\frac{1}{2}$ab.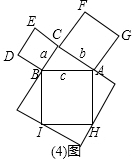 又∵S四邊形ADCB=S△ADB+S△DCB=$\frac{1}{2}$c2+$\frac{1}{2}$a(b-a)
又∵S四邊形ADCB=S△ADB+S△DCB=$\frac{1}{2}$c2+$\frac{1}{2}$a(b-a)
∴$\frac{1}{2}$b2+$\frac{1}{2}$ab=$\frac{1}{2}$c2+$\frac{1}{2}$a(b-a),
∴a2+b2=c2;
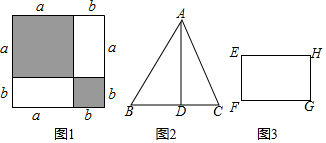
④根據題意,中間小正方形的面積c2=(a+b)2-4×$\frac{1}{2}$×ab=a2+b2;
即在直角三角形中斜邊的平方等于兩直角邊的平方和.
點評 此題考查了勾股定理的證明,勾股定理,多項式的乘法的運用以及由多項式畫圖形的創新題型,此類證明要轉化成同一個圖形的兩種表示方法,從而轉化成方程達到證明的結果.


科目:初中數學 來源:2016-2017學年北京市西城區七年級上學期期末考試數學試卷(解析版) 題型:單選題
甲、乙兩人同時開始采摘櫻桃,甲平均每小時采摘8公斤櫻桃,乙平均每小時采摘7公斤櫻桃。采摘同時結束后,甲從他采摘的櫻桃中取出1公斤給了乙,這時兩人的櫻桃一樣多。他們采摘櫻桃用了多長時間?設他們采摘了x小時,則下面所列方程中正確的是( )
A. 8x-1=7x+1 B. 8x-1=7x C. 8x+l=7x D. 8x+l=7x-1
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
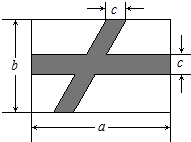 如圖所示,在公園長方形空地上,要修兩條路(圖中的陰影所示),按照圖中標的數據,計算圖中空白部分的面積為( )
如圖所示,在公園長方形空地上,要修兩條路(圖中的陰影所示),按照圖中標的數據,計算圖中空白部分的面積為( )| A. | ab-bc-ac+c2 | B. | bc-ab+ac | C. | b2-bc+a2-ab | D. | a2+ab+bc-ac |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com