
 如圖,在?ABCD的對角線BD上取一點E,使得BE=$\frac{1}{4}$BD,延長AE交BC于G,交DC的延長線于F,求:S△CFG:S△BEG的值.
如圖,在?ABCD的對角線BD上取一點E,使得BE=$\frac{1}{4}$BD,延長AE交BC于G,交DC的延長線于F,求:S△CFG:S△BEG的值. 分析 根據平行四邊形的性質得到AB∥CD,AD∥BC,由平行線分線段成比例定理得到$\frac{GE}{AE}=\frac{BE}{DE}$=$\frac{1}{3}$,$\frac{{S}_{△BEG}}{{S}_{△ABE}}$=$\frac{1}{3}$,得到S△BEG=$\frac{1}{3}$S△BAE,S△CFG=4S△ABG,于是得到結論.
解答 解:∵BE=$\frac{1}{4}$BD,
∴$\frac{BE}{DE}$=$\frac{1}{3}$,
∵四邊形ABCD是平行四邊形,
∴AB∥CD,AD∥BC,
∴$\frac{GE}{AE}=\frac{BE}{DE}$=$\frac{1}{3}$,
∴$\frac{{S}_{△BEG}}{{S}_{△ABE}}$=$\frac{1}{3}$,
∴S△BEG=$\frac{1}{3}$S△BAE,
∵AB∥DF,
∴$\frac{AE}{EF}=\frac{BE}{DE}$=$\frac{AB}{DF}$=$\frac{1}{3}$,
∴$\frac{AB}{CF}$=$\frac{1}{2}$
∴$\frac{{S}_{△ABG}}{{S}_{βCFG}}$=$\frac{1}{4}$,
∴S△CGF=4S△ABG,
∴S△CFG:S△BEG=16:1.
點評 本題考查了平行線分線段成比例定理,平行四邊形的性質,三角形面積的計算,熟練掌握平行線分線段成比例定理是解題的關鍵.


 黃岡創優卷系列答案
黃岡創優卷系列答案科目:初中數學 來源: 題型:填空題
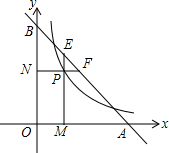 如圖,直線y=6-x交x軸、y軸于A、B兩點,P是反比例函數y=$\frac{k}{x}$(x>0)圖象上位于直線下方的一點,過點P作x軸的垂線,垂足為點M,交AB于點E,過點P作y軸的垂線,垂足為點N,交AB于AB于點F,且AF•BE=8,則k=4.
如圖,直線y=6-x交x軸、y軸于A、B兩點,P是反比例函數y=$\frac{k}{x}$(x>0)圖象上位于直線下方的一點,過點P作x軸的垂線,垂足為點M,交AB于點E,過點P作y軸的垂線,垂足為點N,交AB于AB于點F,且AF•BE=8,則k=4.查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,一次函數y1=x與二次函數y2═ax2+bx+c圖象相交于P,Q兩點,對于函數y3═ax2+(b-1)x+c,有下列結論:
如圖,一次函數y1=x與二次函數y2═ax2+bx+c圖象相交于P,Q兩點,對于函數y3═ax2+(b-1)x+c,有下列結論:| A. | 0個 | B. | 1個 | C. | 2個 | D. | 3個 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
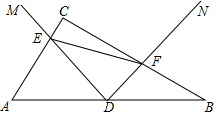 如圖,△ABC中,∠ACB=90°,點D是AB中點,∠MDN=90°,DM交AC于點E,DN交BC于點F.
如圖,△ABC中,∠ACB=90°,點D是AB中點,∠MDN=90°,DM交AC于點E,DN交BC于點F.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
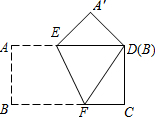 把一張矩形紙片ABCD按如圖所示的方式折疊,使頂點B和D重合,折痕為EF.
把一張矩形紙片ABCD按如圖所示的方式折疊,使頂點B和D重合,折痕為EF.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 2016年我縣九年級學生是總體 | |
| B. | 每一名九年級學生是個體 | |
| C. | 200名九年級學生是總體的一個樣本 | |
| D. | 樣本容量是200 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com