
【題目】在四邊形![]() 中,對角線
中,對角線![]() 、
、![]() 相交于點
相交于點![]() ,將
,將![]() 繞點
繞點![]() 按逆時針方向旋轉得到
按逆時針方向旋轉得到![]() ,旋轉角為θ(0°<θ<90°),連接
,旋轉角為θ(0°<θ<90°),連接![]() 、
、![]() ,
,![]() 與
與![]() 交于點
交于點![]() .
.
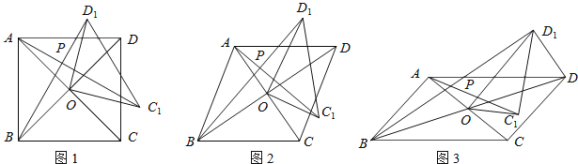
(1)如圖1,若四邊形![]() 是正方形.
是正方形.
①求證:![]() ≌
≌![]() .
.
②請直接寫出![]() 與
與![]() 的位置關系.
的位置關系.
(2)如圖2,若四邊形![]() 是菱形,
是菱形,![]() ,
,![]() ,設
,設![]() .判斷
.判斷![]() 與
與![]() 的位置關系,說明理由,并求出
的位置關系,說明理由,并求出![]() 的值.
的值.
(3)如圖3,若四邊形![]() 是平行四邊形,
是平行四邊形,![]() ,
,![]() ,連接
,連接![]() ,設
,設![]() .請直接寫出
.請直接寫出![]() 的值和
的值和![]() 的值.
的值.
【答案】(1)①證明見解析;②AC1⊥BD1;(2)k=![]() ,AC1⊥BD1,理由見解析;(3)k=
,AC1⊥BD1,理由見解析;(3)k=![]() ,AC12+(kDD1)2=25
,AC12+(kDD1)2=25
【解析】
(1)①根據正方形與旋轉的性質,通過SAS證明兩三角形全等;
②由全等三角形的性質得出![]() ,通過證明
,通過證明![]() 進行求解;
進行求解;
(2)根據菱形與旋轉的性質得出OC1=OA,OD1=OB,∠AOC1=∠BOD1,進而可證明△AOC1∽△BOD1,利用相似三角形的性質進行求解;
(3)同(2)的解法相似可求出k的值,根據旋轉的性質得出OD1=OB=OD,進而可得出![]() ,利用勾股定理進行求解.
,利用勾股定理進行求解.
(1)①證明:∵四邊形ABCD是正方形,
∴OC=OA=OD=OB,AC⊥BD,
∴∠AOB=∠COD=90°,
∵△COD繞點O按逆時針方向旋轉得到△C1OD1,
∴OC1=OC,OD1=OD,∠COC1=∠DOD1,
∴OC1=OD1,∠AOC1=∠BOD1,
在△AOC1和△BOD1中,
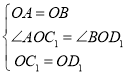 ,
,
∴△AOC1≌△BOD1(SAS);
②解:AC1⊥BD1,理由如下:
∵△AOC1≌△BOD1,
∴![]() ,
,
∵![]() ,
,
∴![]() ,即
,即![]() ,
,
∴AC1⊥BD1;
(2)解:AC1⊥BD1,理由如下:
∵四邊形ABCD是菱形,
∴OC=OA=![]() AC,OD=OB=
AC,OD=OB=![]() BD,AC⊥BD,
BD,AC⊥BD,
∴∠AOB=∠COD=90°,
∵△COD繞點O按逆時針方向旋轉得到△C1OD1,
∴OC1=OC,OD1=OD,∠COC1=∠DOD1,
∴OC1=OA,OD1=OB,∠AOC1=∠BOD1,
∴![]() ,
,
∴△AOC1∽△BOD1,
∴∠OAC1=∠OBD1,
又∵∠AOB=90°,
∴∠OAB+∠ABP+∠OBD1=90°,
∴∠OAB+∠ABP+∠OAC1=90°,
∴∠APB=90°,
∴AC1⊥BD1,
∵△AOC1∽△BOD1,
∴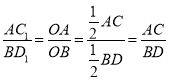 =
=![]() ,
,
∴k=![]() ;
;
(3)解:與(2)一樣可證明△AOC1∽△BOD1,
∴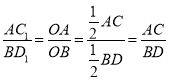
![]() ,
,
∴k=![]() ;
;
∵△COD繞點O按逆時針方向旋轉得到△C1OD1,
∴OD1=OD,而OD=OB,
∴OD1=OB=OD,
∴△BDD1為直角三角形,即![]() ,
,
在Rt△BDD1中,BD12+DD12=BD2=100,
∴(2AC1)2+DD12=100,
∴AC12+(kDD1)2=25.


科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,P是BC上一點,E是AB上一點,PD平分∠APC,PE⊥PD,連接DE交AP于F,在以下判斷中,不正確的是( )
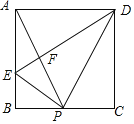
A.當P為BC中點,△APD是等邊三角形
B.當△ADE∽△BPE時,P為BC中點
C.當AE=2BE時,AP⊥DE
D.當△APD是等邊三角形時,BE+CD=DE
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義:在方格紙中,每個小格的頂點叫做格點,以格點為頂點的三角形叫做格點三角形.已知圖1,圖2中的每一個小方格的邊長都為1.
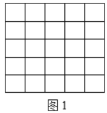
(1)![]() 的三邊長為
的三邊長為![]() ,
,![]() ,
,![]() .
.
①在圖1中畫一個符合題意的![]() ;
;
②求![]() 的邊
的邊![]() 上的高線長;
上的高線長;
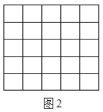
(2)在![]() 的方格紙紙板中最多能剪下(要完整不拼湊)多少個與(1)中
的方格紙紙板中最多能剪下(要完整不拼湊)多少個與(1)中![]() 全等的三角形?并在圖2中設計出來.
全等的三角形?并在圖2中設計出來.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,拋物線的頂點為P(3,—2),且在x軸上截得的線段AB=4.
(1)求拋物線的解析式.
(2)若點Q在拋物線上,且ΔQAB的面積為12,求Q點的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,點A在x軸上,OA=4,將OA繞點O逆時針旋轉120°至OB的位置.
(1)求經過A、O、B三點的拋物線的函數解析式;
(2)在此拋物線的對稱軸上是否存在點P使得以P、O、B三點為頂點的三角形是等腰三角形?若存在,求出點P的坐標;若不存在,請說明理由;
(3 )如圖2,OC=4,⊙A的半徑為2,點M是⊙A上的一個動點,求MC+![]() OM的最小值.
OM的最小值.
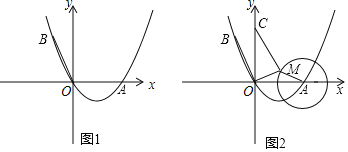
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 與
與![]() 軸交于
軸交于![]() ,
,![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() ,點
,點![]() 與點
與點![]() 關于
關于![]() 軸對稱.
軸對稱.
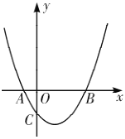
(1)求點![]() ,
,![]() ,
,![]() 的坐標;
的坐標;
(2)求直線![]() 的解析式;
的解析式;
(3)在直線![]() 下方的拋物線上是否存在一點
下方的拋物線上是否存在一點![]() ,使
,使![]() 的面積最大?若存在,求出點
的面積最大?若存在,求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖1,菱形![]() 的頂點
的頂點![]() 、
、![]() 在菱形
在菱形![]() 的邊上,且
的邊上,且![]() ,請直接寫出
,請直接寫出![]() 的結果(不必寫計算過程)
的結果(不必寫計算過程)
(2)將圖1中的菱形![]() 繞點
繞點![]() 旋轉一定角度,如圖2,求
旋轉一定角度,如圖2,求![]() ;
;
(3)把圖2中的菱形都換成矩形,如圖3,且![]() ,此時
,此時![]() 的結果與(2)小題的結果相比有變化嗎?如果有變化,直接寫出變化后的結果(不必寫計算過程);若無變化,請說明理由.
的結果與(2)小題的結果相比有變化嗎?如果有變化,直接寫出變化后的結果(不必寫計算過程);若無變化,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法正確的是( )
A.“打開電視機,正在播世界杯足球賽”是必然事件
B.甲組數據的方差是![]() ,乙組數據的方差是
,乙組數據的方差是![]() ,則乙組數據比甲組數據穩定
,則乙組數據比甲組數據穩定
C.一組數據2,3,4,5,5,6的眾數和中位數都是5
D.“擲一枚硬幣,正面朝上的概率是0.5”表示每拋擲硬幣2次就有1次正面朝上
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】給定一個函數,如果這個函數的圖象上存在一個點,它的橫、縱坐標相等,那么這個點叫做該函數的不變點.
(1)一次函數![]() 的不變點的坐標為______.
的不變點的坐標為______.
(2)二次函數![]() 的兩個不變點分別為點
的兩個不變點分別為點![]() (
(![]() 在
在![]() 的左側),將點
的左側),將點![]() 繞點
繞點![]() 順時針旋轉90°得到點
順時針旋轉90°得到點![]() ,求點
,求點![]() 的坐標.
的坐標.
(3)已知二次函數![]() 的兩個不變點的坐標為
的兩個不變點的坐標為![]() .
.
①求![]() 的值;
的值;
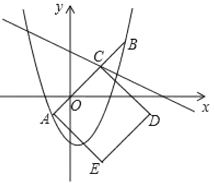
②如圖,設拋物線![]() 與線段
與線段![]() 圍成的封閉圖形記作
圍成的封閉圖形記作![]() .點
.點![]() 為一次函數
為一次函數![]() 的不變點,以線段
的不變點,以線段![]() 為邊向下作正方形
為邊向下作正方形![]() .當
.當![]() 兩點中只有一個點在封閉圖形
兩點中只有一個點在封閉圖形![]() 的內部(不包含邊界)時,求出
的內部(不包含邊界)時,求出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com