
【題目】給定一個函數,如果這個函數的圖象上存在一個點,它的橫、縱坐標相等,那么這個點叫做該函數的不變點.
(1)一次函數![]() 的不變點的坐標為______.
的不變點的坐標為______.
(2)二次函數![]() 的兩個不變點分別為點
的兩個不變點分別為點![]() (
(![]() 在
在![]() 的左側),將點
的左側),將點![]() 繞點
繞點![]() 順時針旋轉90°得到點
順時針旋轉90°得到點![]() ,求點
,求點![]() 的坐標.
的坐標.
(3)已知二次函數![]() 的兩個不變點的坐標為
的兩個不變點的坐標為![]() .
.
①求![]() 的值;
的值;
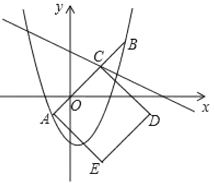
②如圖,設拋物線![]() 與線段
與線段![]() 圍成的封閉圖形記作
圍成的封閉圖形記作![]() .點
.點![]() 為一次函數
為一次函數![]() 的不變點,以線段
的不變點,以線段![]() 為邊向下作正方形
為邊向下作正方形![]() .當
.當![]() 兩點中只有一個點在封閉圖形
兩點中只有一個點在封閉圖形![]() 的內部(不包含邊界)時,求出
的內部(不包含邊界)時,求出![]() 的取值范圍.
的取值范圍.
【答案】(1)(1,1);(2)![]() ,
,![]() ;(3)①
;(3)①![]() ,②
,②![]() 或
或![]()
【解析】
(1)聯立一次函數y=3x﹣2與y=x組成方程組,解之即可得出結論;
(2)聯立二次函數y=x2﹣3x+1與y=x組成方程組,解之即可得出點P、Q的坐標,由點P、Q在直線y=x上,可得出△PQR為等腰直角三角形,過點P作PP′⊥QR,垂足為點P′,根據等腰直角三角形的性質即可得出點R的坐標;
(3)①根據點A、B的坐標,利用待定系數法即可求出a、b的值;
②聯立一次函數y=﹣![]() x+m與y=x成方程組,解之即可得出點C的坐標,根據正方形的性質可得出點D、E的坐標,分只有點D在圖形M的內部及只有點E在圖形M的內部兩種情況找出關于m的不等式組,解之即可得出結論(對于只寫答案不寫過程的可以直接代入點D、E的坐標,利用極限法找出m的取值范圍).
x+m與y=x成方程組,解之即可得出點C的坐標,根據正方形的性質可得出點D、E的坐標,分只有點D在圖形M的內部及只有點E在圖形M的內部兩種情況找出關于m的不等式組,解之即可得出結論(對于只寫答案不寫過程的可以直接代入點D、E的坐標,利用極限法找出m的取值范圍).
解:(1)根據題意得:![]() ,
,
解得:![]() ,
,
∴一次函數y=3x﹣2的不動點的坐標為(1,1).
(2)根據題意得:![]() ,
,
解得: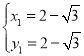 ,
,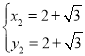 ,
,
![]() ,
,![]() ,
,![]() ,
,![]() .
.
∵點P、Q在直線y=x上,
∴∠QPR=45°,
∴△PQR為等腰直角三角形.
過點P作PP′⊥QR,垂足為點P′,如圖1所示.
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() .
.
(3)①∵二次函數y=ax2+bx﹣3的兩個不變點的坐標為A(﹣1,﹣1)、B(3,3),
![]()
![]() ,
,
解得:![]() .
.
②![]()
 ,解得:
,解得: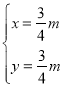 ,
,
![]() 點
點![]() 的坐標為
的坐標為![]() ,
,![]() .
.
∵四邊形ACDE為正方形,點A、C在直線y=x上,A(﹣1,﹣1),
![]() ,
,![]() ,點
,點![]() ,
,![]() .
.
當只有點![]() 在圖形
在圖形![]() 的內部時,有
的內部時,有 ,
,
解得![]() ;
;
當只有點![]() 在圖形
在圖形![]() 的內部時,有
的內部時,有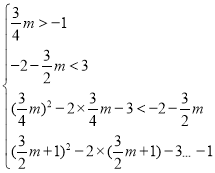 ,
,
解得:![]() .
.
綜上所述:![]() 的取值范圍為
的取值范圍為![]() 或
或![]() .
.



 尖子生新課堂課時作業系列答案
尖子生新課堂課時作業系列答案 英才計劃同步課時高效訓練系列答案
英才計劃同步課時高效訓練系列答案科目:初中數學 來源: 題型:
【題目】在四邊形![]() 中,對角線
中,對角線![]() 、
、![]() 相交于點
相交于點![]() ,將
,將![]() 繞點
繞點![]() 按逆時針方向旋轉得到
按逆時針方向旋轉得到![]() ,旋轉角為θ(0°<θ<90°),連接
,旋轉角為θ(0°<θ<90°),連接![]() 、
、![]() ,
,![]() 與
與![]() 交于點
交于點![]() .
.
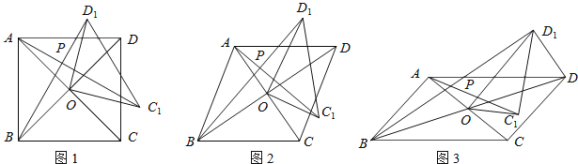
(1)如圖1,若四邊形![]() 是正方形.
是正方形.
①求證:![]() ≌
≌![]() .
.
②請直接寫出![]() 與
與![]() 的位置關系.
的位置關系.
(2)如圖2,若四邊形![]() 是菱形,
是菱形,![]() ,
,![]() ,設
,設![]() .判斷
.判斷![]() 與
與![]() 的位置關系,說明理由,并求出
的位置關系,說明理由,并求出![]() 的值.
的值.
(3)如圖3,若四邊形![]() 是平行四邊形,
是平行四邊形,![]() ,
,![]() ,連接
,連接![]() ,設
,設![]() .請直接寫出
.請直接寫出![]() 的值和
的值和![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
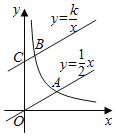
【題目】如圖,直線y=![]() x與雙曲線y=
x與雙曲線y=![]() (k>0,x>0)交于點A,將直線y=
(k>0,x>0)交于點A,將直線y=![]() x向上平移2個單位長度后,與y軸交于點C,與雙曲線交于點B,若OA=3BC,則k的值為____.
x向上平移2個單位長度后,與y軸交于點C,與雙曲線交于點B,若OA=3BC,則k的值為____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2019年3月25日是全國中小學生安全教育日,前進中學為加強學生的安全意識,組全校學生參加安全知識競賽,從中抽取了部分學生成績(得分取正整數,滿分為100分),各等級進行統計(![]() 級.
級.![]() 分-
分-![]() 分;
分;![]() 級.
級.![]() 分
分![]() 分;
分;![]() 級.
級.![]() 分
分![]() 分;
分;![]() 級.
級.![]() 分
分![]() 分;
分;![]() 級.
級.![]() 分
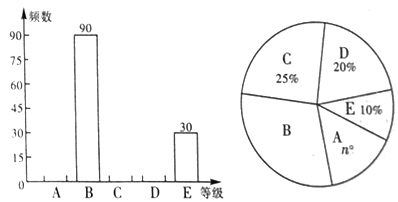
分![]() 分),并將統計結果繪制成如下兩幅尚不完整的統計圖,請你結合圖中所給信息解答下列問題:
分),并將統計結果繪制成如下兩幅尚不完整的統計圖,請你結合圖中所給信息解答下列問題:
(1)![]() _______.
_______.
(2)補全頻數分布直方圖;
(3)該校共有![]() 名學生.若成績在
名學生.若成績在![]() 分以下(含
分以下(含![]() 分)的學生安全意識不強,有待進.步加強安全教育,則該校安全意識不強的學生約有多少名?
分)的學生安全意識不強,有待進.步加強安全教育,則該校安全意識不強的學生約有多少名?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】汽車產業的發展,有效促進我國現代化建設.某汽車銷售公司2016年盈利1500萬元,到2018年盈利2160萬元,且從2016年到2018年,每年盈利的年增長率相同.
(1)求每年盈利的年增長率;
(2)若該公司盈利的年增長率繼續保持不變,那么2019年該公司盈利能否達到2500萬元?
查看答案和解析>>
科目:初中數學 來源: 題型:
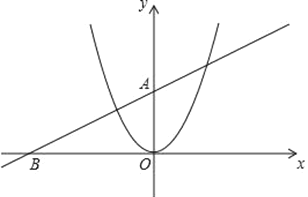
【題目】已知直線y=kx+b經過點A(0,2),B(﹣4,0)和拋物線y=x2.
(1)求直線的解析式;
(2)將拋物線y=x2沿著x軸向右平移,平移后的拋物線對稱軸左側部分與y軸交于點C,對稱軸右側部分拋物線與直線y=kx+b交于點D,連接CD,當CD∥x軸時,求平移后得到的拋物線的解析式;
(3)在(2)的條件下,平移后得到的拋物線的對稱軸與x軸交于點E,P為該拋物線上一動點,過點P作拋物線對稱軸的垂線,垂足為Q,是否存在這樣的點P,使以點E,P,Q為頂點的三角形與△AOB相似?若存在,請求出點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】[閱讀理解]
我們知道:![]() ,那么
,那么![]() 結果等于多少呢?
結果等于多少呢?
在圖1所示的等邊三角形數陣中,第![]() 行的一個小等邊三角形中的數為
行的一個小等邊三角形中的數為![]() ,即
,即![]() 第
第![]() 行的三個小等邊三角形中的數的和是
行的三個小等邊三角形中的數的和是![]() 即
即![]() ; ..第
; ..第![]() 行的
行的![]() 個小等邊三角形中的數的和是
個小等邊三角形中的數的和是![]() 個,即
個,即![]() ,該等邊三角形數陣中共有
,該等邊三角形數陣中共有![]() 小等邊三角形,所有小等邊三角形數的和為
小等邊三角形,所有小等邊三角形數的和為![]() .
.
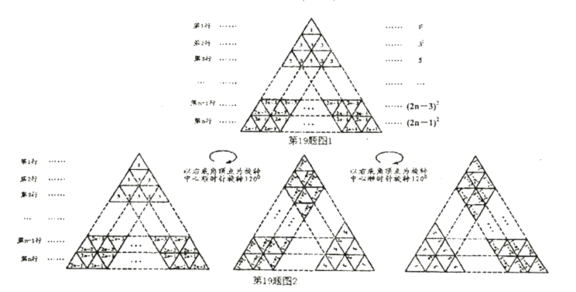
[規律探究]
以圖1中的等邊三角形數陣的右底角頂點為旋轉中心順時針旋轉![]() 再把旋轉后的圖形按同樣的方法可得如圖2所示的三角形數陣,觀察這三個等邊三角形數陣各行同一位置的小等邊三角形中的數,發現位于奇數位置的三個數(如第
再把旋轉后的圖形按同樣的方法可得如圖2所示的三角形數陣,觀察這三個等邊三角形數陣各行同一位置的小等邊三角形中的數,發現位于奇數位置的三個數(如第![]() 行的第
行的第![]() 個小三角形中的數分別為
個小三角形中的數分別為![]() 的和為
的和為![]() ;發現位于偶數位置的三個數(如第
;發現位于偶數位置的三個數(如第![]() 行的第
行的第![]() 個小三角形中的數分別為
個小三角形中的數分別為![]() 的和為
的和為![]() ;而每個等邊三角形數陣中,由于位于奇數位置的數比位于偶數位置的數多
;而每個等邊三角形數陣中,由于位于奇數位置的數比位于偶數位置的數多![]() 個,則位于偶數位置的數有_
個,則位于偶數位置的數有_
個![]()
因此,![]()
[解決問題]根據以上發現,計算:![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于二次函數![]() ,下列說法正確的個數是( )
,下列說法正確的個數是( )
①對于任何滿足條件的![]() ,該二次函數的圖象都經過點
,該二次函數的圖象都經過點![]() 和
和![]() 兩點;
兩點;
②若該函數圖象的對稱軸為直線![]() ,則必有
,則必有![]() ;
;
③當![]() 時,
時,![]() 隨
隨![]() 的增大而增大;
的增大而增大;
④若![]() ,
,![]() 是函數圖象上的兩點,如果
是函數圖象上的兩點,如果![]() 總成立,則
總成立,則![]() .
.
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校對交通法則的了解情況在全校隨機調查了部分學生,調查結果分為四種:![]() .非常了解,
.非常了解,![]() .比較了解,
.比較了解,![]() .基本了解,
.基本了解,![]() .不太了解,并將此次調查結果整理繪制成下面不完整的條形統計圖和扇形統計圖.
.不太了解,并將此次調查結果整理繪制成下面不完整的條形統計圖和扇形統計圖.
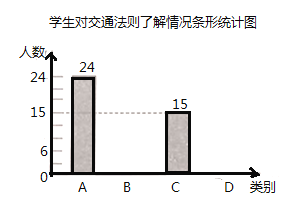
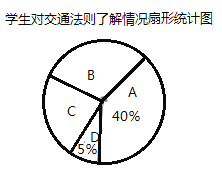
(1)本次共調查_______名學生;扇形統計圖中![]() 所對應扇形的圓心角度數是_______;
所對應扇形的圓心角度數是_______;
(2)補全條形統計圖;
(3)學校準備從甲、乙、丙、丁四位學生中隨機抽取兩名學生參加市區交通法規競賽,請用列表或畫樹狀圖的方法求甲和乙兩名學生同時被選中的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com