
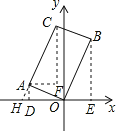
【題目】如圖,在矩形AOBC中,點A的坐標是(-2,1),點C的縱坐標是4,求B、C兩點的坐標.

【答案】點C的坐標為![]() .
.
【解析】首先過點A作AD⊥x軸于點D,過點B作BE⊥x軸于點E,過點C作CF∥y軸,過點A作AF∥x軸,交點為F,易得△CAF≌△BOE,△AOD∽△OBE,然后由相似三角形的對應邊成比例,求得答案.
過點A作AD⊥x軸于點D,過點B作BE⊥x軸于點E,過點C作CF∥y軸,過點A作AF∥x軸,交點為F,延長CA交x軸于點H,
∵四邊形AOBC是矩形,
∴AC∥OB,AC=OB,
∴∠CAF=∠BOE=∠CHO,
在△ACF和△OBE中,
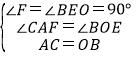 ,
,
∴△CAF≌△BOE(AAS),
∴BE=CF=4-1=3,
∵∠AOD+∠BOE=∠BOE+∠OBE=90°,
∴∠AOD=∠OBE,
∵∠ADO=∠OEB=90°,
∴△AOD∽△OBE,
∴![]() ,
,
即![]() ,
,
∴OE=![]() ,
,
即點B(![]() ,3),
,3),
∴AF=OE=![]() ,
,
∴點C的橫坐標為:-(2-![]() )=-
)=-![]() ,
,
∴點C(-![]() ,4).
,4).


科目:初中數學 來源: 題型:
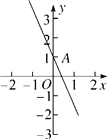
【題目】如圖,在平面直角坐標系中,一次函數y=-2x+1的圖象與y軸交于點A.
(1)若點A關于x軸的對稱點B在一次函數y=![]() x+b的圖象上,求b的值,并在同一坐標系中畫出該一次函數的圖象;
x+b的圖象上,求b的值,并在同一坐標系中畫出該一次函數的圖象;
(2)求這兩個一次函數的圖象與y軸圍成的三角形的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
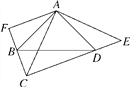
【題目】如圖,∠BAD=∠CAE=90°,AB=AD,AE=AC,點D在CE上,AF⊥CB,垂足為F.
(1)若AC=10,求四邊形ABCD的面積;
(2)求證:CE=2AF.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:關于x的方程x2-2(m+1)x+m2=0.
(1)當m取何值時,方程有兩個實數根?
(2)為m選取一個合適的整數,使方程有兩個不相等的實數根,并求這兩個根.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若一次函數y=kx+b與反比例函數y= ![]() 的圖像如圖所示,則關于x的不等式kx+b﹣
的圖像如圖所示,則關于x的不等式kx+b﹣ ![]() ≤﹣2的解集為( )
≤﹣2的解集為( ) 
A.0<x≤2或x≤﹣4
B.﹣4≤x<0或x≥2
C.![]() ≤x<0或x
≤x<0或x ![]()
D.x ![]() 或0
或0 ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
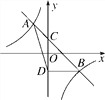
【題目】如圖,一次函數y=k1x+b與反比例函數y=![]() (k2≠0)相交于A(-1,2),B(2,m)兩點,與y軸相交于點C.
(k2≠0)相交于A(-1,2),B(2,m)兩點,與y軸相交于點C.
(1)求k1、k2、m的值;
(2)若點D與點C關于x軸對稱,求△ABD的面積;
(3)若M(x1,y1)、N(x2、y2)是反比例函數y=![]() 圖象上的兩點,且x1<x2時,y1>y2,指出點M、N各位于坐標系的哪個象限,并簡要說明理由.
圖象上的兩點,且x1<x2時,y1>y2,指出點M、N各位于坐標系的哪個象限,并簡要說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個盒子里有標號分別為1,2,3,4的四個球,這些球除標號數字外都相同.
(1)從盒中隨機摸出一個小球,求摸到標號數字為奇數的球的概率;
(2)甲、乙兩人用這六個小球玩摸球游戲,規則是:甲從盒中隨機摸出一個小球,記下標號數字后放回盒里,充分搖勻后,乙再從盒中隨機摸出一個小球,并記下標號數字.若兩次摸到球的標號數字同為奇數或同為偶數,則判甲贏;若兩次摸到球的標號數字為一奇一偶,則判乙贏.請用列表法或畫樹狀圖的方法說明這個游戲對甲、乙兩人是否公平.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某單位在十月份準備組織部分員工到北京旅游,現聯系了甲、乙兩家旅行社,兩家旅行社報價均為 4000 元/人,兩家旅行社同時又對 10 人以上的團體推出了優惠舉 措:甲旅行社對每位員工七五折優惠;而乙旅行社是免去一位員工的費用,其余員工八 折優惠.
(1)如果設參加旅游的員工共有 n(n>10)人,則甲旅行社的費用為 元,乙旅 行社的費用為 元;(用含 n 的代數式表示)
(2)假如這個單位現組織共 30 名員工到旅游,該單位選擇哪一家旅行社比較優惠?請通 過計算說明理由.
(3)如果計劃在十月份外出旅游七天,這七天的日期之和(不包含月份)為 105,則他們 于十月 號出發.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com