輕巧奪冠周測月考直通中考系列答案科目：初中數學 來源： 題型：
如圖，雙曲線
經過四邊形OABC的頂點A、C，∠ABC＝90°，OC平分OA與x軸正半
軸的夾角，AB∥x軸，將△ABC沿AC翻折后得到△AB＇C，B＇點落在OA上，則四邊形OABC的面積是 .
 |
查看答案和解析>>
科目：初中數學 來源： 題型：
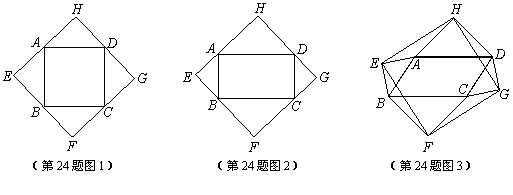
以四邊形ABCD的邊AB、BC、CD、DA為斜邊分別向外側作等腰直角三角形，直角頂點分別為E、F、G、H，順次連結這四個點，得四邊形EFGH．
(1)如圖1，當四邊形ABCD為正方形時，我們發現四邊形EFGH是正方形；
如圖2，當四邊形ABCD為矩形時，請判斷：四邊形EFGH的形狀（不要求證明）；
(2)如圖3，當四邊形ABCD為一般平行四邊形時，
① 求證：HE=HG；
② 四邊形EFGH是什么四邊形？并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
倡導研究性學習方式，著力教材研究，習題研究，是學生跳出題海，提高學習能力和創新能力的有效途徑。下面是一案例，請同學們認真閱讀、研究，完成“類比猜想”及后面的問題。
習題解答：
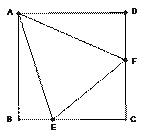
習題 如圖（1），點E、F分別在正方形ABCD的邊BC、CD上，∠EAF=45°，連接EF，則EF=BE+DF，說明理由。
習題研究
觀察分析 觀察圖（1），由解答可知，該題有用的條件是①ABCD是四邊形，點E、F分別在邊BC、CD上；②AB=AD；③∠B=∠D=90°；
④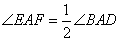
。答：成立。
類比猜想
（1）在四邊形ABCD中，點E、F分別在BC、CD上，當AB=AD，
∠B=∠D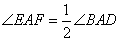，時，還有EF=BE+DF嗎？答：不一定成立。
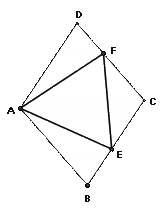
研究一個問題，常從特例入手，請同學們研究：如圖（2），在菱
形ABCD中，點E、F分別在BC、CD上，當∠BAD=120°，∠EAF=60°
時，還有EF=BE+DF嗎？
（2）在四邊形ABCD中，點E、F分別在BC、CD上，當AB=AD，∠B+∠D=180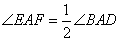，時，EF=BE+DF嗎？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
，其中x＝
．
（k≠0）的圖象經過點P（-2，-1），則該反比例函數的解析式是
，∠ABC的平分線與∠BCD的平分線交于點P，則∠P= 
B. 
C. 
D. 
中，
，有一個銳角為60°，BC=6，若P在直線AC上（不與點A，C重合）,且
,則CP的長為_______