
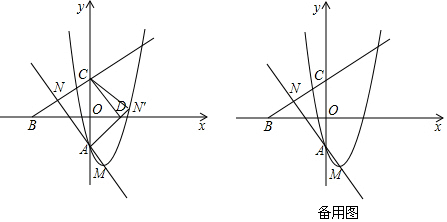
分析 (1)已知了拋物線的解析式,不難用公式法求出M的坐標為(1,-a-1).由于拋物線過A點,因此A的坐標是(0,-a).根據A,M的坐標,用待定系數法可得出直線AM的解析式為y=-x-a.直線AM和y=$\frac{1}{2}$x+a聯立方程組即可求出N的坐標.
(2)根據折疊的性質不難得出N與N′正好關于y軸對稱,得出N′的坐標.由于N′在拋物線上,因此將N′的坐標代入拋物線的解析式中即可得出a的值.也就能確定N,C的坐標.求出△ANC和△ADC的面積,即可得出△CDN的面積;
(3)本題可分兩種情況進行討論:
①當P在y軸左側時,如果使以P,N,A,C為頂點的四邊形為平行四邊形,那么P需要滿足的條件是PN平行且相等于AC,也就是說,如果N點向上平移AC個單位即2a后得到的點就是P點.然后將此時P的坐標代入拋物線中,如果沒有解說明不存在這樣的點P,如果能求出a的值,那么即可求出此時P的坐標.
②當P在y軸右側時,P需要滿足的條件是PN與AC應互相平分(平行四邊形的對角線互相平分),那么NP必過原點,且關于原點對稱.那么可得出此時P的坐標,然后代入拋物線的解析式中按①的方法求解即可.
解答  解:(1)M(1,-a-1),N(-$\frac{4}{3}$a,$\frac{1}{3}$a);
解:(1)M(1,-a-1),N(-$\frac{4}{3}$a,$\frac{1}{3}$a);
故答案為:1,-a-1;-$\frac{4}{3}$a,$\frac{1}{3}$a;
(2)∵由題意得點N與點N′關于y軸對稱,
∴N′($\frac{4}{3}$a,$\frac{1}{3}$a).
將N′的坐標代入y=x2-2x-a得:$\frac{1}{3}$a=$\frac{16}{9}$a2-$\frac{8}{3}$a-a,
∴a1=0(不合題意,舍去),a2=$\frac{9}{4}$.
∴N(-3,$\frac{3}{4}$),
∴點N到y軸的距離為3.
∵A(0,-$\frac{9}{4}$),N'(3,$\frac{3}{4}$),
∴直線AN'的解析式為y=x-$\frac{9}{4}$,它與x軸的交點為D($\frac{9}{4}$,0),
∴點D到y軸的距離為$\frac{9}{4}$.
由題知,A(0,a),C(0,-a),
∴點A,C關于x軸對稱,
∴AC=2AO,
∴S△CDN=S△ACN-S△ACD=$\frac{1}{2}$×$\frac{9}{2}$×3-$\frac{1}{2}$×$\frac{9}{2}$×$\frac{9}{4}$=$\frac{27}{16}$;
(3)存在,理由如下:
①當點P在y軸的左側時,若四邊形ACPN是平行四邊形,
則PN∥AC,PN=AC,
則把N向上平移2a個單位得到P,坐標為(-$\frac{4}{3}$a,$\frac{7}{3}$a),
代入拋物線的解析式,得:$\frac{7}{3}$a=$\frac{16}{9}$a2+$\frac{8}{3}$a-a,
解得a1=0(不舍題意,舍去),a2=$\frac{3}{8}$,
則P(-$\frac{1}{2}$,$\frac{7}{8}$);
②當點P在y軸的右側時,若四邊形APCN是平行四邊形,則AC與PN互相平分,
則OA=OC,OP=ON.
則P與N關于原點對稱,則P($\frac{4}{3}$a,-$\frac{1}{3}$a);
將P點坐標代入拋物線解析式得:-$\frac{1}{3}$a=$\frac{16}{9}$a2-$\frac{8}{3}$a-a,
解得a1=0(不合題意,舍去),a2=$\frac{15}{8}$,
則P($\frac{5}{2}$,-$\frac{5}{8}$).
故存在這樣的點P(-$\frac{1}{2}$,$\frac{7}{8}$)或P($\frac{5}{2}$,-$\frac{5}{8}$),能使得以P,A,C,N為頂點的四邊形是平行四邊形.
點評 本題是二次函數綜合題目,著重考查了待定系數法求函數解析式、圖形旋轉變換、平行四邊形的性質等重要知識點,綜合性強,能力要求較高.考查學生分類討論,數形結合的數學思想方法.


 芝麻開花課程新體驗系列答案
芝麻開花課程新體驗系列答案科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
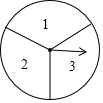 如圖,一個轉盤被分成3等分,每一份上各寫有一個數字,隨機轉動轉盤2次,第一次轉到的數字數字為十位數字,第二次轉到的數字為個位數字,2次轉動后組成一個兩位數(若指針停在等分線上則重新轉一次)
如圖,一個轉盤被分成3等分,每一份上各寫有一個數字,隨機轉動轉盤2次,第一次轉到的數字數字為十位數字,第二次轉到的數字為個位數字,2次轉動后組成一個兩位數(若指針停在等分線上則重新轉一次)查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com