
 如圖,初三一班數(shù)學(xué)興趣小組的同學(xué)欲測量公園內(nèi)一棵樹DE的高度,他們在這棵樹正前方一座樓亭前的臺階上A點處測得樹頂端D的仰角為30°.朝著這棵樹的方向走到臺階下的點C處,測得樹頂端D的仰角為60°,已知A點的高度AB為2米,臺階AC的坡度為1:$\sqrt{3}$(即AB:BC=1:$\sqrt{3}$),且B,C,E三點在同一條直線上,請根據(jù)以上條件求出樹DE的高度.(測量器的高度忽略不計)
如圖,初三一班數(shù)學(xué)興趣小組的同學(xué)欲測量公園內(nèi)一棵樹DE的高度,他們在這棵樹正前方一座樓亭前的臺階上A點處測得樹頂端D的仰角為30°.朝著這棵樹的方向走到臺階下的點C處,測得樹頂端D的仰角為60°,已知A點的高度AB為2米,臺階AC的坡度為1:$\sqrt{3}$(即AB:BC=1:$\sqrt{3}$),且B,C,E三點在同一條直線上,請根據(jù)以上條件求出樹DE的高度.(測量器的高度忽略不計) 分析 由于AF⊥AB,則四邊形ABEF為矩形,設(shè)DE=x,在Rt△CDE中,CE=$\frac{DE}{tan∠DCE}$=$\frac{DE}{tan60°}$=$\frac{\sqrt{3}}{3}$x,在Rt△ABC中,得到$\frac{AB}{BC}$=$\frac{1}{\sqrt{3}}$,求出BC,在Rt△AFD中,求出AF,由AF=BC+CE即可求出x的長.
解答 解:∵AF⊥AB,AB⊥BE,DE⊥BE,
∴四邊形ABEF為矩形,
∴AF=BE,EF=AB=2
設(shè)DE=x,在Rt△CDE中,CE=$\frac{DE}{tan∠DCE}$=$\frac{DE}{tan60°}$=$\frac{\sqrt{3}}{3}$x,
在Rt△ABC中,
∵$\frac{AB}{BC}$=$\frac{1}{\sqrt{3}}$,AB=2,
∴BC=2$\sqrt{3}$,
在Rt△AFD中,DF=DE-EF=x-2,
∴AF=$\frac{DF}{tan∠DAF}$=$\frac{x-2}{tan30°}$=$\sqrt{3}$(x-2),
∵AF=BE=BC+CE.
∴$\sqrt{3}$(x-2)=2$\sqrt{3}$+$\frac{\sqrt{3}}{3}$x,
解得x=6.
答:樹DE的高度為6米.
點評 本題考查了解直角三角形的應(yīng)用--仰角、坡度問題、矩形的判定與性質(zhì)、三角函數(shù);借助仰角構(gòu)造直角三角形并解直角三角形是解決問題的關(guān)鍵.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
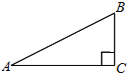 如圖,在Rt△ABC中,∠ABC=90°,BC=1,AC=$\sqrt{5}$.
如圖,在Rt△ABC中,∠ABC=90°,BC=1,AC=$\sqrt{5}$.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
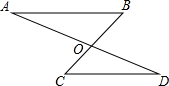 如圖,已知AB∥CD,AD與BC相交于點O,∠B=40°,∠D=34°,則∠AOC=( )
如圖,已知AB∥CD,AD與BC相交于點O,∠B=40°,∠D=34°,則∠AOC=( )| A. | 40° | B. | 34° | C. | 74° | D. | 90° |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com