
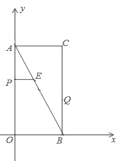
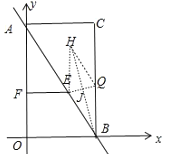
【題目】如圖,在平面直角坐標系中,已知矩形![]() 的頂點
的頂點![]() 的坐標是
的坐標是![]() ,動點
,動點![]() 從點
從點![]() 出發,沿線段
出發,沿線段![]() 向終點
向終點![]() 運動,同時動點
運動,同時動點![]() 從點
從點![]() 出發,沿線段
出發,沿線段![]() 向終點
向終點![]() 運動.點
運動.點![]() 、
、![]() 的運動速度均為每秒1個單位,過點
的運動速度均為每秒1個單位,過點![]() 作
作![]() 交
交![]() 于點
于點![]() ,一點到達,另一點即停.設點
,一點到達,另一點即停.設點![]() 的運動時間為
的運動時間為![]() 秒
秒![]() .
.
(1)填空:用含![]() 的代數式表示下列各式
的代數式表示下列各式
![]() __________,
__________,![]() __________.
__________.
(2)①當![]() 時,求點
時,求點![]() 到直線
到直線![]() 的距離.
的距離.
②當點![]() 到直線
到直線![]() 的距離等于
的距離等于![]() 時,直接寫出
時,直接寫出![]() 的值.
的值.
(3)在動點![]() 、
、![]() 運動的過程中,點
運動的過程中,點![]() 是矩形
是矩形![]() (包括邊界)內一點,且以
(包括邊界)內一點,且以![]() 、
、![]() 、
、![]() 、
、![]() 為頂點的四邊形是菱形,直接寫出點
為頂點的四邊形是菱形,直接寫出點![]() 的橫坐標.
的橫坐標.
【答案】(1)![]() ;(2)2;(3)
;(2)2;(3)![]() 或
或![]() ;(4)
;(4)![]() ,
,![]() .
.
【解析】
(1)根據C點坐標(2,4)可知AC=OB=2,AO=BC=4,根據P,Q的運動速度即可表示出AP,CQ的長;
(2)①延長PE交BC于H點,再求出直線AB的解析式,根據![]() 求出E點坐標,得到AP的長求出時間t,故可得到Q點坐標,即可求出點
求出E點坐標,得到AP的長求出時間t,故可得到Q點坐標,即可求出點![]() 到直線
到直線![]() 的距離;
的距離;
②分別表示出Q,H的坐標,根據![]() ,列出方程即可求解;
,列出方程即可求解;
(3)分兩種情形依據菱形的鄰邊相等關系構建方程即可解決問題.
(1)∵C(2,4)
∴AC=OB=2,AO=BC=4,
∵動點![]() 從點
從點![]() 出發,沿線段
出發,沿線段![]() 向終點
向終點![]() 運動,同時動點
運動,同時動點![]() 從點
從點![]() 出發,沿線段
出發,沿線段![]() 向終點
向終點![]() 運動.點
運動.點![]() 、
、![]() 的運動速度均為每秒1個單位,
的運動速度均為每秒1個單位,
∴AP=t,CQ=BC-BQ=4-t,
故答案為:t;4-t;
(2)設直線AB的解析式為y=kx+b,把A(0,4),B(2,0)代入得![]() ,
,
解得 ![]() ,
,
∴直線AB的解析式為y=2x+4.
![]()
∴E(![]() ,3)
,3)
∴AP=AO-OP=4-3=1=t
∴Q(2,1),BQ=1
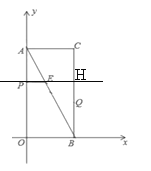
延長PE交BC于H點,∴BH=PO=3
故QH=BH-BQ=3-1=2;
②點![]() 到直線
到直線![]() 的距離等于
的距離等于![]() 時,即
時,即![]()
由AP=CH=t,BQ=t,
得H(2,4-t),Q(2,t)
∴![]()
解得![]() 或
或![]()
(3)∵OP=4-t,故E點的縱坐標為4-t,代入直線AB得E(![]() t,4t)
t,4t)
又Q(2,t),
①如圖,當QE=QB時,可得四邊形EQBH是菱形,
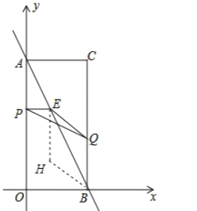
∴EQ2=BQ2
(2![]() t)2+[t-(4t)]2=t2,
t)2+[t-(4t)]2=t2,
整理得:13t272t+80=0,
解得t=![]() 或4(舍棄),
或4(舍棄),
![]() t=
t=![]()
∴點![]() 的橫坐標是
的橫坐標是![]() ;
;
②當BE=BQ時,如圖,可得四邊形BQHE是菱形.
EB2=BQ2
(![]() t-2)2+(4t-0)2=t2,
t-2)2+(4t-0)2=t2,
整理得:t240t+80=0,
解得t=![]() 或
或![]() (舍棄),
(舍棄),
![]() t=
t=![]()
∴點![]() 的橫坐標是
的橫坐標是![]() ;
;
綜上,點![]() 的橫坐標是
的橫坐標是![]() 或
或![]() .
.


科目:初中數學 來源: 題型:
【題目】(9分)九年級數學興趣小組經過市場調查,得到某種運動服每月的銷量與售價的相關信息如下表:
售價(元/件) | 100 | 110 | 120 | 130 | … |
月銷量(件) | 200 | 180 | 160 | 140 | … |
已知該運動服的進價為每件60元,設售價為![]() 元.
元.
(1)請用含x的式子表示:①銷售該運動服每件的利潤是 元;②月銷量是 件;(直接寫出結果)
(2)設銷售該運動服的月利潤為![]() 元,那么售價為多少時,當月的利潤最大,最大利潤是多少?
元,那么售價為多少時,當月的利潤最大,最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
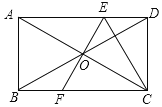
【題目】如圖,矩形ABCD,兩條對角線相交于O點,過點O作AC的垂線EF,分別交AD、BC于E、F點,連結CE,若OC![]() cm,CD=4cm,則DE的長為( )
cm,CD=4cm,則DE的長為( )
A.![]() cmB.5cmC.3cmD.2cm
cmB.5cmC.3cmD.2cm
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】體育文化公司為某學校捐贈甲、乙兩種品牌的體育器材,甲品牌有A、B、C三種型號,乙品牌有D、E兩種型號,現要從甲、乙兩種品牌的器材中各選購一種型號進行捐贈.
(1)下列事件是不可能事件的是 .
A.選購乙品牌的D型號 B.既選購甲品牌也選購乙品牌
C.選購甲品牌的A型號和乙品牌的D型號 D.只選購甲品牌的A型號
(2)寫出所有的選購方案(用列表法或樹狀圖);
(3)如果在上述選購方案中,每種方案被選中的可能性相同,那么A型器材被選中的概率是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一條公路旁依次有![]() ,
,![]() ,
,![]() 三個村莊,甲乙兩人騎自行車分別從
三個村莊,甲乙兩人騎自行車分別從![]() 村、
村、![]() 村同時出發前往
村同時出發前往![]() 村,甲乙之間的距離
村,甲乙之間的距離![]() 與騎行時間
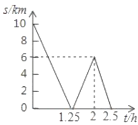
與騎行時間![]() 之間的函數關系如圖所示,下列結論:
之間的函數關系如圖所示,下列結論:
①![]() ,
,![]() 兩村相距
兩村相距![]() ; ②出發
; ②出發![]() 后兩人相遇;
后兩人相遇;
③甲每小時比乙多騎行![]() ; ④相遇后,乙又騎行了
; ④相遇后,乙又騎行了![]() 時兩人相距
時兩人相距![]() .
.
其中正確的有_____________________.(填序號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,若將△ABC繞點C順時針旋轉180°得到△EFC,連接AF、BE.
(1)求證:四邊形ABEF是平行四邊形;
(2)當∠ABC為多少度時,四邊形ABEF為矩形?請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,O為原點,點A(2,0),點P(1,m)(m>0)和點Q關于x軸對稱.過點P作PB∥x軸,與直線AQ交于點B,如果AP⊥BO,求點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個不透明的口袋中裝有4個完全相同的小球,分別標有數字1,2,3,4,另外有一個可以自由旋轉的圓盤,被分成面積相等的3個扇形區域,分別標有數字1,2,3(如圖所示).

(1)從口袋中摸出一個小球,所摸球上的數字大于2的概率為 ;
(2)小龍和小東想通過游戲來決定誰代表學校參加歌詠比賽,游戲規則為:一人從口袋中摸出一個小球,另一人轉動圓盤,如果所摸球上的數字與圓盤上轉出數字之和小于5,那么小龍去;否則小東去.你認為游戲公平嗎?請用樹狀圖或列表法說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
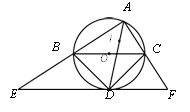
【題目】如圖,A是以BC為直徑的⊙O上一點,I是△ABC的內心,AI的延長線交⊙O于點D,過點D作BC的平行線交AB、AC的延長線于E、F.下列說法:①△DBC是等腰直角三角形;②EF與⊙O相切;③EF=2BC;④點B、I、C在以點D 為圓心的同一個圓上.其中一定正確的是_______(把你認為正確結論的序號都填上)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com