
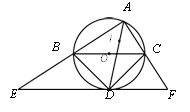
【題目】如圖,A是以BC為直徑的⊙O上一點,I是△ABC的內心,AI的延長線交⊙O于點D,過點D作BC的平行線交AB、AC的延長線于E、F.下列說法:①△DBC是等腰直角三角形;②EF與⊙O相切;③EF=2BC;④點B、I、C在以點D 為圓心的同一個圓上.其中一定正確的是_______(把你認為正確結論的序號都填上)
【答案】①②④
【解析】
根據內心的定義得到∠BAD=∠CAD,再根據圓周角定理得到BD=CD,即可判斷①;
根據直角三角形的性質即可判斷②,根據三角形的中位線性質判斷③即可,連接BI、CI,根據三角形的內心及三角形的外角的性質求出DB=DI,即可判斷④.
∵I是△ABC的內心,
∴∠BAD=∠CAD,
∴BD=CD,
∵BC為⊙O的直徑,
∴∠BDC=90°,
∴△DBC是等腰直角三角形,故①正確;
連接OD,
∵BC為⊙O的直徑,BD=CD,
∴OD⊥BC,
∵EF∥BC,
∴OD⊥EF,
∴EF與⊙O相切,故②正確;
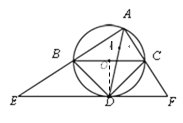
∵點B、C不是AE和AF的中點,
∴BC不是△AEF的中位線,
∴![]() ,故③錯誤;
,故③錯誤;
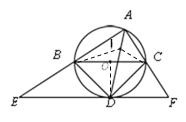
連接BI、CI,
∵I是△ABC的內心,
∴∠ABI=∠CBI,
∵∠BAD=∠CAD=∠CBD,
∴∠CBD+∠CBI=∠BAD+∠ABI,
∴∠DBI=∠DIB,
∴DB=DI=DC,
∴點B、I、C在以點D 為圓心的同一個圓上,故④正確.


科目:初中數學 來源: 題型:
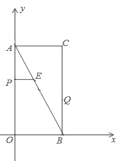
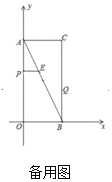
【題目】如圖,在平面直角坐標系中,已知矩形![]() 的頂點
的頂點![]() 的坐標是
的坐標是![]() ,動點
,動點![]() 從點
從點![]() 出發,沿線段
出發,沿線段![]() 向終點
向終點![]() 運動,同時動點
運動,同時動點![]() 從點
從點![]() 出發,沿線段
出發,沿線段![]() 向終點
向終點![]() 運動.點
運動.點![]() 、
、![]() 的運動速度均為每秒1個單位,過點
的運動速度均為每秒1個單位,過點![]() 作
作![]() 交
交![]() 于點
于點![]() ,一點到達,另一點即停.設點
,一點到達,另一點即停.設點![]() 的運動時間為
的運動時間為![]() 秒
秒![]() .
.
(1)填空:用含![]() 的代數式表示下列各式
的代數式表示下列各式
![]() __________,
__________,![]() __________.
__________.
(2)①當![]() 時,求點
時,求點![]() 到直線
到直線![]() 的距離.
的距離.
②當點![]() 到直線
到直線![]() 的距離等于
的距離等于![]() 時,直接寫出
時,直接寫出![]() 的值.
的值.
(3)在動點![]() 、
、![]() 運動的過程中,點
運動的過程中,點![]() 是矩形
是矩形![]() (包括邊界)內一點,且以
(包括邊界)內一點,且以![]() 、
、![]() 、
、![]() 、
、![]() 為頂點的四邊形是菱形,直接寫出點
為頂點的四邊形是菱形,直接寫出點![]() 的橫坐標.
的橫坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下面材料,完成(1)﹣(3)題
數學課上,老師出示了這樣一道題:如圖,四邊形ABCD,AD∥BC,AB=AD,E為對角線AC上一點,∠BEC=∠BAD=2∠DEC,探究AB與BC的數量關系.
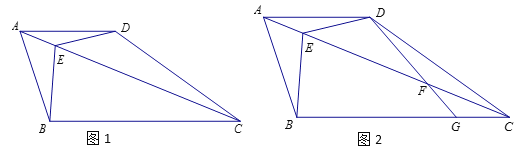
某學習小組的同學經過思考,交流了自己的想法:
小柏:“通過觀察和度量,發現∠ACB=∠ABE”;
小源:“通過觀察和度量,AE和BE存在一定的數量關系”;
小亮:“通過構造三角形全等,再經過進一步推理,就可以得到線段AB與BC的數量關系”.
……
老師:“保留原題條件,如圖2, AC上存在點F,使DF=CF=![]() AE,連接DF并延長交BC于點G,求
AE,連接DF并延長交BC于點G,求![]() 的值”.
的值”.
(1)求證:∠ACB=∠ABE;
(2)探究線段AB與BC的數量關系,并證明;
(3)若DF=CF=![]() AE,求
AE,求![]() 的值(用含k的代數式表示).
的值(用含k的代數式表示).
查看答案和解析>>
科目:初中數學 來源: 題型:
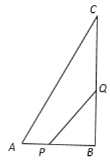
【題目】如圖,△ABC中,∠B=90°,AB=12,BC=16,點P從點A開始沿邊AB向點B以1cm/s的速度移動,與此同時,點Q從點B開始沿邊BC向點C以2cm/s的速度移動.如果P、Q分別從A、B同時出發,當點Q運動到點C時,兩點停止運動,問:
(1)經過幾秒后,△PBQ的面積等于20cm2?
(2)△PBQ的面積會等于△ABC的面積的一半嗎?若會,請求出此時的運動時間;若不會,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
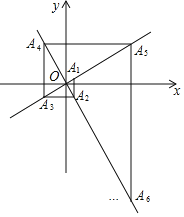
【題目】如圖,在平面直角坐標系中,函數y=![]() x和y=﹣
x和y=﹣![]() x的圖象分別為直線l1,l2,過l1上的點A1(1,
x的圖象分別為直線l1,l2,過l1上的點A1(1,![]() )作x軸的垂線交l2于點A2,過點A2作y軸的垂線交l1于點A3,過點A3作x軸的垂線交l2于點A4,…依次進行下去,則點A2019的橫坐標為_____.
)作x軸的垂線交l2于點A2,過點A2作y軸的垂線交l1于點A3,過點A3作x軸的垂線交l2于點A4,…依次進行下去,則點A2019的橫坐標為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(動手操作)
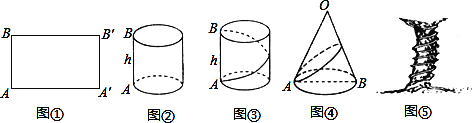
如圖①,把長為l、寬為h的矩形卷成以AB為高的圓柱形,則點A′與點______重合,點B′與點______重合;
(探究發現)
如圖②,圓柱的底面周長是80,高是60,若在圓柱體的側面繞一圈絲線作裝飾,從下底面A出發,沿圓柱側面繞一周到上底面B,則這條絲線最短的長度是______;
(實踐應用)
如圖③,圓錐的母線長為12,底面半徑為4,若在圓錐體的側面繞一圈彩帶做裝飾,從圓錐的底面上的點A出發,沿圓錐側面繞一周回到點A.求這條彩帶最短的長度是多少?
(拓展聯想)
如圖④,一顆古樹上下粗細相差不大,可以看成圓柱體.測得樹干的周長為3米,高為18米,有一根紫藤自樹底部均勻的盤繞在樹干上,恰好繞8周到達樹干的頂部,這條紫藤至少有 米
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】第二十四屆冬季奧林匹克運動會將與2022年2月20日在北京舉行,北京將成為歷史上第一座舉辦過夏奧會又舉辦過冬奧會的城市,東寶區舉辦了一次冬奧會知識網上答題競賽,甲、乙兩校各有400名學生參加活動,為了解這兩所學校的成績情況,進行了抽樣調查,過程如下,請補充完整.
(收集數據)
從甲、乙兩校各隨機抽取20名學生,在這次競賽中它們的成績如下:
甲 | 30 | 60 | 60 | 70 | 60 | 80 | 30 | 90 | 100 | 60 |
60 | 100 | 80 | 60 | 70 | 60 | 60 | 90 | 60 | 60 | |
乙 | 80 | 90 | 40 | 60 | 80 | 80 | 90 | 40 | 80 | 50 |
80 | 70 | 70 | 70 | 70 | 60 | 80 | 50 | 80 | 80 |
(整理、描述數據)按如下分數段整理、描述這兩組樣本數據:
(說明:優秀成績為80<x≤100,良好成績為50<x≤80,合格成績為30≤x≤50.)
學校 | 平均分 | 中位數 | 眾數 |
甲 | 67 | 60 | 60 |
乙 | 70 | 75 | a |
30≤x≤50 | 50<x≤80 | 80<x≤100 | |
甲 | 2 | 14 | 4 |
乙 | 4 | 14 | 2 |
(分析數據)兩組樣本數據的平均分、中位數、眾數如右表所示:其中a= .
(得出結論)
(1)小偉同學說:“這次競賽我得了70分,在我們學校排名屬中游略偏上!”由表中數據可知小明是 校的學生;(填“甲”或“乙”)
(2)老師從乙校隨機抽取一名學生的競賽成績,試估計這名學生的競賽成績為優秀的概率為 ;
(3)根據以上數據推斷一所你認為競賽成績較好的學校,并說明理由.(至少從兩個不同的角度說明推斷的合理性)
查看答案和解析>>
科目:初中數學 來源: 題型:
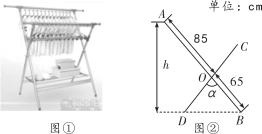
【題目】有一種落地晾衣架如圖①所示,其原理是通過改變兩根支撐桿夾角的度數來調整晾衣桿的高度.圖②是支撐桿的平面示意圖,AB和CD分別是兩根不同長度的支撐桿,夾角∠BOD=α.若AO=85 cm,BO=DO=65 cm.問:當α=74°時,較長支撐桿的端點A離地面的高度h約為______cm.(參考數據:sin 37°≈0.6,cos 37°≈0.8,sin 53°≈0.8,cos 53°≈0.6)
查看答案和解析>>
科目:初中數學 來源: 題型:
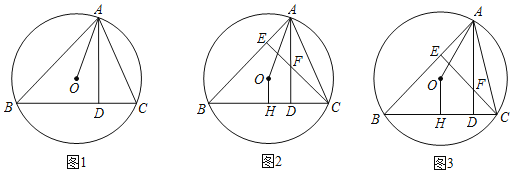
【題目】已知銳角△ABC內接于⊙O,AD⊥BC于點D,連接AO.
(1)如圖1,求證:∠BAO=∠CAD;
(2)如圖2,CE⊥AB于點E,交AD于點F,過點O作OH⊥BC于點H,求證:AF=2OH;
(3)如圖3,在(2)的條件下,若AF=AO,tan∠BAO=![]() ,BC=
,BC=![]() ,求AC的長.
,求AC的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com