
【題目】如圖所示,在長方形ABCD中,AB=6厘米,BC=12厘米,點P沿AB邊從點A開始向點B以1厘米/秒的速度移動,點Q沿BC從點B開始向點C以2厘米/秒的速度移動,如果P、Q同時出發,用t(秒)表示移動的時間(0≤t≤6).
(1)當PB=2厘米時,求點P移動多少秒?
(2)t為何值時,△PBQ為等腰直角三角形?
(3)求四邊形PBQD的面積,并探究一個與計算結果有關的結論.
【答案】
(1)解:∵PB=2cm,AB=6cm, ∴AP=AB-PB=6-2=4(秒), 即點P移動4秒
(2)解:∵△PBQ為等腰直角三角形, ∴PB=BQ,即6-t=2t,解得t=2, ∴當t的值為2秒時,△PBQ為等腰直角三角形
(3)解:由題意可知AP=t,AB=6,BQ=2t,BC=12, ∴PB=6-t,QC=12-2t,CD=6,AD=12, ∴S△APD= ![]() APAD=
APAD= ![]() t×12=6t, S△QCD=
t×12=6t, S△QCD= ![]() QCCD=
QCCD= ![]() (12-2t)6=36-6t, ∴S四邊形PBQD=S矩形ABCD-S△APD-S△QCD=72-6t-(36-6t)=36, 結論:不論P、Q怎樣運動總有四邊形PBQD的面積等于長方形ABCD面積的一半
(12-2t)6=36-6t, ∴S四邊形PBQD=S矩形ABCD-S△APD-S△QCD=72-6t-(36-6t)=36, 結論:不論P、Q怎樣運動總有四邊形PBQD的面積等于長方形ABCD面積的一半
【解析】(1)知道AB、PB的長,可求出AP,再根據點P運動的速度可求點P運動的時間;(2)當BP=BQ時,△PBQ為等腰直角三角形,用t將BP、BQ表示出來,列方程可求解;(3)四邊形PBQD可看作矩形ABCD-![]() APD-
APD-![]() DCQ得到,于是有S四邊形PBQD=S矩形ABCD-S△APD-S△QCD可求解。
DCQ得到,于是有S四邊形PBQD=S矩形ABCD-S△APD-S△QCD可求解。


科目:初中數學 來源: 題型:
【題目】如圖,一次函數![]() 的圖象與
的圖象與![]() 軸、
軸、![]() 軸分別交于點
軸分別交于點![]() ,以線段
,以線段![]() 為邊在第一象限作等邊
為邊在第一象限作等邊![]() .
.
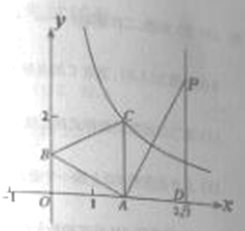
(1)若點![]() 在反比例函數
在反比例函數![]() 的圖象上,求該反比例函數的解析式;
的圖象上,求該反比例函數的解析式;
(2)點![]() 在第一象限,過點
在第一象限,過點![]() 作
作![]() 軸的垂線,垂足為
軸的垂線,垂足為![]() ,當
,當![]() 與
與![]() 相切時,
相切時,![]() 點是否在(1)中反比例函數圖象上,如果在,求出
點是否在(1)中反比例函數圖象上,如果在,求出![]() 點坐標;如果不在,請加以說明.
點坐標;如果不在,請加以說明.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com