
分析 (1)根據題意得出第1行的每個數為-2的序數次冪,據此可得;
(2)由題意知,第2行每個數比第1行相應的數大2及第3行的每個數是第1行相應數的倒數的2倍與對應奇數的積,據此可得;
(3)①列出p的代數式,將m=9代入可得;②根據|p+4000|=|(-2)m+(-2)m+2+$\frac{2(2m-1)}{(-2)^{m}}$+4000|=|2(-2)m+$\frac{4m-2}{(-2)^{m}}$+4002|,若m為偶數,則m越大|p+4000|的值越大,可知m應為奇數,分別求出m=9、11、13時的值可得答案.
解答 解:(1)∵第1個數-2=(-2)1,第2個數4=(-2)2,第3個數-8=(-2)3,…
∴第8個數為(-2)8=256,
故答案為:256;
(2)由題意知,第2行每個數比第1行相應的數大2,
∴若第一行的第n個數用(-2)n表示,則第二行第n個數表示為(-2)n+2;
∵第3行的每個數是第1行相應數的倒數的2倍與對應奇數的積,
∴第三行的第n個數表示為$\frac{2(2n-1)}{{{{(-2)}^n}}}$,
故答案為:(-2)n+2,$\frac{2(2n-1)}{{{{(-2)}^n}}}$;
(3)①當m=9時,p=(-2)8+(-2)8+2+$\frac{2×(2×9-1)}{(-2)^{9}}$=-1022$\frac{17}{256}$;
∵|p+4000|=|(-2)m+(-2)m+2+$\frac{2(2m-1)}{(-2)^{m}}$+4000|=|2(-2)m+$\frac{4m-2}{(-2)^{m}}$+4002|,
若m為偶數,則m越大,|p+4000|的值越大;
∴m應為奇數,
則當m=9時,|p+4000|=|-1022$\frac{17}{256}$+4000|=3977$\frac{239}{256}$,
當m=11時,|p+4000|=97$\frac{21}{1024}$,
當m=13時,|p+4000|=-12382$\frac{5}{1024}$,
∴m=11時,|p+4000|的值最小,
故答案為:11.
點評 本題主要考查數字的變化規律,根據題意得出第1行的每個數為-2的序數次冪、第2行每個數比第1行相應的數大2及第3行的每個數是第1行相應數的倒數的2倍與對應奇數的積是解題的關鍵.


科目:初中數學 來源: 題型:選擇題
 如圖是小明畫的正方體表面展開圖,由7個相同的正方形組成.小穎認為小明畫的不對,她剪去其中的一個正方形后,得到的平面圖就可以折成一個正方體.小穎剪去的正方形的編號是( )
如圖是小明畫的正方體表面展開圖,由7個相同的正方形組成.小穎認為小明畫的不對,她剪去其中的一個正方形后,得到的平面圖就可以折成一個正方體.小穎剪去的正方形的編號是( )| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在平面直角坐標系中,已知△ABC的三個頂點的坐標分別為A(1,0)、B(4,0)、C(5,2).將△ABC繞著點A按逆時針方向旋轉90度得到△A1B1C1
如圖,在平面直角坐標系中,已知△ABC的三個頂點的坐標分別為A(1,0)、B(4,0)、C(5,2).將△ABC繞著點A按逆時針方向旋轉90度得到△A1B1C1查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
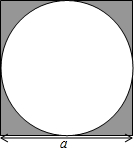 如圖,一個邊長為a的正方形內畫了一個圓,其直徑也是a
如圖,一個邊長為a的正方形內畫了一個圓,其直徑也是a查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com