

分析 (1)直接判斷△DCB≌△DCM即可得出結論;
(2)由對稱得出BD=AD,結合(1)的結論得出AD=DM,最后用面積公式即可得出結論;
(3)先用△BCQ∽△BHO,得出$\frac{BC}{BH}=\frac{BQ}{BO}$①,再用角平分線定理得出$\frac{BC}{AC}=\frac{BQ}{AQ}$②,再用平行線分線段成比例定理即可得出$\frac{CG}{AC}=\frac{OQ}{AQ}$④,進而用這三個比例式即可得出結論.
解答 解:(1)如圖1,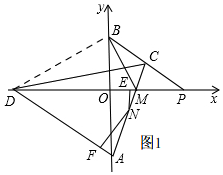 連接BD,
連接BD,
∵CD平分∠ACB交x軸于點D,
∴∠DCB=∠DCM,
在△DCB和△DCM中,$\left\{\begin{array}{l}{CB=CM}\\{∠DCB=∠DCM}\\{CD=CD}\end{array}\right.$,
∴△DCB≌△DCM,
∴BD=MD,
(2)NE+NF的值是不發(fā)生變化,
理由:如圖2,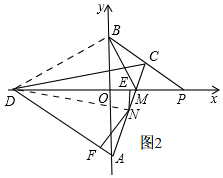 連接BD,DN,
連接BD,DN,
∵A、B(0,2)兩點關于x軸對稱,
∴BD=AD,
由(1)知,BD=MD,
∴AD=MD,
∵NE⊥PD于E,NF⊥AD于F,
∴S△ADM=S△DMN+S△DAN=$\frac{1}{2}$DM•NE+$\frac{1}{2}$AD•NF=$\frac{1}{2}$DM•NE+$\frac{1}{2}$DM•NF=$\frac{1}{2}$DM•(NE+NF),
∵OA⊥DM.
∴S△ADM=$\frac{1}{2}$DM•OA,
∴$\frac{1}{2}$DM•(NE+NF)=$\frac{1}{2}$DM•OA,
∴NE+NF=OA,
∵B(0,2),
∴OB=2,
∵A、B(0,2)兩點關于x軸對稱,
∴OA=OB=2,
∴NE+NF=2.
即:NE+NF是定值,為2;
(3)$\frac{AC-BH}{CG}$的值是不發(fā)生變化,
理由:如圖3,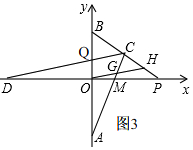 ,∵A、B(0,2)兩點關于x軸對稱,
,∵A、B(0,2)兩點關于x軸對稱,
∴OA=OB=2,
∵OH∥CD,
∴△BCQ∽△BHO,
∴$\frac{BC}{BH}=\frac{BQ}{BO}$①
∵CD平分∠ACB交x軸于點D.
∴$\frac{BC}{AC}=\frac{BQ}{AQ}$②,
∴②÷①得,$\frac{BH}{AC}=\frac{BO}{AQ}$③,
∵OH∥CD,
∴$\frac{CG}{AC}=\frac{OQ}{AQ}$④,
∴③÷④得,$\frac{BH}{CG}=\frac{BO}{OQ}$⑤,
∴$\frac{AC-BH}{CG}$=$\frac{AC}{CG}-\frac{BH}{CG}$=$\frac{AQ}{OQ}$-$\frac{BO}{OQ}$=$\frac{AQ-BO}{OQ}$=$\frac{OA+OQ-BO}{OQ}$=1.
即:$\frac{AC-BH}{CG}$的值是定值,為1.
點評 此題是幾何變換綜合題,主要考查了全等三角形的判定和性質,軸對稱,平行線分線段成比例定理,相似三角形的判定和性質,角平分線的性質定理,解本題的關鍵是得出比例式,幾個比例的處理得出結論是解本題的難點.


科目:初中數學 來源: 題型:解答題
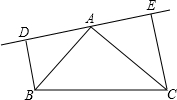 如圖,在△ABC中,AB=AC,DE是過點A的直線,BD⊥DE于D,CE⊥DE于點E;若B,C在DE的同側(如圖所示)且AD=CE.求證:AB⊥AC.
如圖,在△ABC中,AB=AC,DE是過點A的直線,BD⊥DE于D,CE⊥DE于點E;若B,C在DE的同側(如圖所示)且AD=CE.求證:AB⊥AC.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
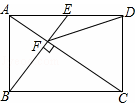 如圖,在矩形ABCD中,E是AD邊的中點,BE⊥AC于點F,連接DF,分析下列五個結論:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$;⑤S四邊形CDEF=$\frac{5}{2}$S△ABF,其中正確的結論有①②③⑤.
如圖,在矩形ABCD中,E是AD邊的中點,BE⊥AC于點F,連接DF,分析下列五個結論:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$;⑤S四邊形CDEF=$\frac{5}{2}$S△ABF,其中正確的結論有①②③⑤.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
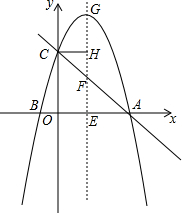 已知拋物線y=ax2+bx+4與x軸交于A,B兩點,與y軸交于點C,點B的坐標為(-1,0),過x軸上一點E作EG⊥x軸交拋物線于點G,交直線AC于點F.
已知拋物線y=ax2+bx+4與x軸交于A,B兩點,與y軸交于點C,點B的坐標為(-1,0),過x軸上一點E作EG⊥x軸交拋物線于點G,交直線AC于點F.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
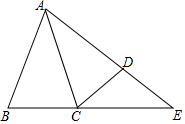 如圖△ABC中,AB=AC=8,∠BAC=30°,現將△ABC繞點A逆時針旋轉30°得到△ACD,延長AD、BC交于點E,則DE的長是4$\sqrt{3}$-4.
如圖△ABC中,AB=AC=8,∠BAC=30°,現將△ABC繞點A逆時針旋轉30°得到△ACD,延長AD、BC交于點E,則DE的長是4$\sqrt{3}$-4.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
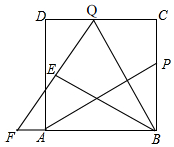 如圖,P為邊長為6的正方形ABCD的邊BC上一動點(P與B、C不重合),Q在CD上,且CQ=BP,連接AP、BQ,將△BQC沿BQ所在的直線翻折得到△BQE,延長QE交BA的延長線于點F.
如圖,P為邊長為6的正方形ABCD的邊BC上一動點(P與B、C不重合),Q在CD上,且CQ=BP,連接AP、BQ,將△BQC沿BQ所在的直線翻折得到△BQE,延長QE交BA的延長線于點F.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 在平面直角坐標系xOy中,拋物線y=-x2+mx+n與x軸交于點A,B(A在B的左側).
在平面直角坐標系xOy中,拋物線y=-x2+mx+n與x軸交于點A,B(A在B的左側).查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com