
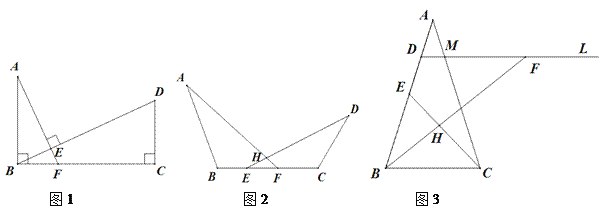
【題目】(1)【特殊發現】如圖1,AB⊥BC于B,CD⊥BC于C,連接BD,過A作AF⊥BD,交BD于E,交BC于F,若BF=1,BC=3,則AB·CD= ;
(2)【類比探究】如圖2,在線段BC上存在點E,F,連接AF,DE交于點H,若∠ABC=∠AHD=∠ECD,求證:AB·CD=BF·CE;
(3)【解決問題】如圖3,在等腰△ABC中,AB=AC=4,E為AB中點,D為AE中點,過點D作直線DM∥BC,在直線DM上取一點F,連接BF交CE于點H,使∠FHC=∠ABC,問:DF·BC是否為定值?若是,請求出,若不是,請說明理由.
【答案】(1)3;(2)詳見解析;(3)是,DF·BC=12,理由詳見解析.
【解析】試題分析:(1)先由余角的性質得到∠A=∠CBD,從而△ABF∽△BCD,再根據相似三角形的性質列比例式求解;(2)由∠ABC=∠AHD=∠ECD,得到∠AFB=∠EDC,從而△ABF∽△ECD,
再根據相似三角形的性質列比例式求解;(3)法一,在DA的延長線上取一點N,使∠DNF=∠ABC,然后由△FDN∽△ABC和△NFB∽△BEC,得到![]() 和
和![]() ,然后整理即可得到結論;法二,取BC的中點K,連接EK,由E為AB中點,然后由△FDB∽△EKC,得到
,然后整理即可得到結論;法二,取BC的中點K,連接EK,由E為AB中點,然后由△FDB∽△EKC,得到![]() ,然后結合法一整理即可得到結論;法三,延長FD,CE交于點G,由法一得:∠ADM=∠AMD,∠ABF=∠ECB,然后由△GMC∽△BDF和△GED∽△CEB,得到
,然后結合法一整理即可得到結論;法三,延長FD,CE交于點G,由法一得:∠ADM=∠AMD,∠ABF=∠ECB,然后由△GMC∽△BDF和△GED∽△CEB,得到![]() 和
和![]() ,然后整理即可得到結論;
,然后整理即可得到結論;
解: (1) ∵AB⊥BC,AF⊥BD,
∴∠A+∠AFB=90°, ∠CBD+∠AFB=90°,
∴∠A=∠CBD,
又∵∠ABF=∠C,
∴△ABF∽△BCD,
![]() ,
,
∴ AB·CD=BC·BF=3.
(2)容易由∠ABC=∠AHD=∠ECD,得到∠AFB=∠EDC,
從而△ABF∽△ECD,
那么AB·CD=BF·CE;
(3)法一:(模型法)解:是,DF·BC=12,
理由如下:
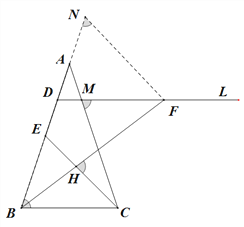
如圖,在DA的延長線上取一點N,使∠DNF=∠ABC,
由AB=AC,DM∥BC,可得:∠ADM=∠AMD=∠ABC=∠ACB∠FMC=∠DNF,
∴△FDN∽△ABC,且DF=NF,∴![]() 即NF·BC=ND·AB,
即NF·BC=ND·AB,
又由∠ABC=∠FHC,得∠ABF+∠FBC=∠FBC+∠ECB,
∴∠ABF=∠ECB,∴△NFB∽△BEC,
∴![]() 即NF·BC=NB·BE,
即NF·BC=NB·BE,
∴NB·BE=ND·AB,依題意得:AD=DE=1,BE=2,
∴NB·2=ND·4,∴NB=2ND,∴ND=BD=3,
∴NB=6,∴NF·BC=6×2=12即DF·BC=12。
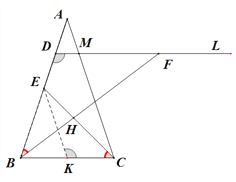
法二:(平行法)取BC的中點K,連接EK,由E為AB中點,
∴EK![]()
![]() AC,得∠ADM=∠ABC=∠EKB,
AC,得∠ADM=∠ABC=∠EKB,
∴∠BDF=∠EKC,再由法一可知:∠DBF=∠ECB,
∴△FDB∽△EKC,∴![]() ,即DF·CK=EK·DB,
,即DF·CK=EK·DB,
由法一得:DB=3,EK=BE=2,CK=![]() BC,
BC,
∴DF·![]() BC=2×3,∴DF·BC=12。
BC=2×3,∴DF·BC=12。
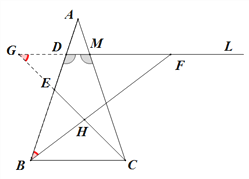
法三:延長FD,CE交于點G,由法一得:∠ADM=∠AMD,∠ABF=∠ECB,
∴∠BDM=∠CMD,又∵DF∥BC,∴∠G=∠ECB,∴∠G=∠ABF,
∴△GMC∽△BDF,∴![]() ,∴DF·GM=MC·DB=3×3=9,
,∴DF·GM=MC·DB=3×3=9,
又∵GD∥BC,DE=1,BE=2,
∴△GED∽△CEB,∴![]() ,
,
同理![]() ,∴GM=GD+DM=
,∴GM=GD+DM=![]() BC+
BC+![]() BC=
BC=![]() BC,
BC,
∴DF·![]() BC=9,∴DF·BC=12。
BC=9,∴DF·BC=12。


 新課標階梯閱讀訓練系列答案
新課標階梯閱讀訓練系列答案 口算心算速算應用題系列答案
口算心算速算應用題系列答案科目:初中數學 來源: 題型:
【題目】請從以下兩個小題中任選一題作答,若多選,則按第一題計分.
(A)兒童節期間,文具商店搞促銷活動,同時購買一個書包和一個文具盒可以打8折優惠,能比標價省13.2元,已知書包標價比文具盒標價的3倍少6元.那么設一個文具盒標價為x元,依據題意列方程得________.
(B)用科學記算器計算: ![]() ________(計算結果保留兩位小數).
________(計算結果保留兩位小數).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,弦CD⊥AB于點E,AM是△ACD的外角∠DAF的平分線.

(1)求證:AM是⊙O的切線;
(2)若∠D = 60°,AD = 2,射線CO與AM交于N點,請寫出求ON長的思路.
查看答案和解析>>
科目:初中數學 來源: 題型:
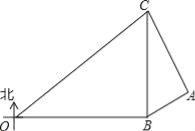
【題目】在某次海上軍事學習期間,我軍為確保△OBC海域內的安全,特派遣三艘軍艦分別在O、B、C處監控△OBC海域,在雷達顯示圖上,軍艦B在軍艦O的正東方向80海里處,軍艦C在軍艦B的正北方向60海里處,三艘軍艦上裝載有相同的探測雷達,雷達的有效探測范圍是半徑為r的圓形區域.(只考慮在海平面上的探測)
(1)若三艘軍艦要對△OBC海域進行無盲點監控,則雷達的有效探測半徑r至少為多少海里?
(2)現有一艘敵艦A從東部接近△OBC海域,在某一時刻軍艦B測得A位于北偏東60°方向上,同時軍艦C測得A位于南偏東30°方向上,求此時敵艦A離△OBC海域的最短距離為多少海里?
(3)若敵艦A沿最短距離的路線以20![]() 海里/小時的速度靠近△OBC海域,我軍軍艦B沿北偏東15°的方向行進攔截,問B軍艦速度至少為多少才能在此方向上攔截到敵艦A?
海里/小時的速度靠近△OBC海域,我軍軍艦B沿北偏東15°的方向行進攔截,問B軍艦速度至少為多少才能在此方向上攔截到敵艦A?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】當k值相同時,我們把正比例函數![]() 與反比例函數
與反比例函數![]() 叫做“關聯函數”.
叫做“關聯函數”.
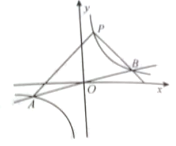
(1)如圖,若k>0,這兩個函數圖象的交點分別為A,B,求點A,B的坐標(用k表示);
(2)若k=1,點P是函數![]() 在第一象限內的圖象上的一個動點(點P不與B重合),設點P的坐標為(
在第一象限內的圖象上的一個動點(點P不與B重合),設點P的坐標為(![]() ),其中m>0且m≠2.作直線PA,PB分別與x軸交于點C,D,則△PCD是等腰三角形,請說明理由;
),其中m>0且m≠2.作直線PA,PB分別與x軸交于點C,D,則△PCD是等腰三角形,請說明理由;
(3)在(2)的基礎上,是否存在點P使△PCD為直角三角形?若存在,請求出點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學校準備用9萬元購進50臺電視機,為了節省費用,學校打算以出廠價從廠家直接采購,已知廠家生產三種不同型號的電視機,出廠價分別為:甲種每臺1500元,乙種每臺2100元,丙種每臺2500元.
(1)若學校同時購進其中兩種不同型號電視機共50臺,用去9萬元,請研究一下學校的采購方案;
(2)若學校去商場購買,在出廠價相同的情況下,商場銷售一臺甲種電視機獲利150元,銷售一臺乙種電視機獲利200元,銷售一臺丙種電視機獲利250元,在(1)的條件下,學校選擇哪種方案省下的錢最多?
(3)若學校準備用9萬元同時購進三種不同的電視機50臺,請你設計進貨方案(直接寫出方案)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某社會團體準備購進甲、乙兩種防護服捐給一線抗疫人員,經了解,購進5件甲種防護服和4件乙種防護服需要2萬元,購進10件甲種防護服和3件乙種防護服需要3萬元.
(1)甲種防護服和乙種防護服每件各多少元?
(2)實際購買時,發現廠家有兩種優惠方案,方案一:購買甲種防護服超過20件時,超過的部分按原價的8折付款,乙種防護服沒有優惠;方案二:兩種防護服都按原價的9折付款,該社會團體決定購買![]()
![]() 件甲種防護服和30件乙種防護服.
件甲種防護服和30件乙種防護服.
①求兩種方案的費用![]() 與件數
與件數![]() 的函數解析式;
的函數解析式;
②請你幫該社會團體決定選擇哪種方案更合算.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點D在AC上,點F、G分別在AC、BC的延長線上,CE平分∠ACB交BD于點O,且∠EOD+∠OBF=180°,∠F=∠G.則圖中與∠ECB相等的角有( )
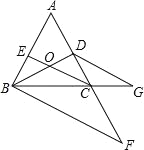
A. 6個 B. 5個 C. 4個 D. 3個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)已知∠AOB=25°42′,則∠AOB的余角為 ,∠AOB的補角為 ;
(2)已知∠AOB=α,∠BOC=β,OM平分∠AOB,ON平分∠BOC,用含α,β的代數式表示∠MON的大小;
(3)如圖,若線段OA與OB分別為同一鐘表上某一時刻的時針與分針,且∠AOB=25°,則經過多少時間后,△AOB的面積第一次達到最大值.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com