
【題目】如圖,AB是⊙O的直徑,弦CD⊥AB于點E,AM是△ACD的外角∠DAF的平分線.

(1)求證:AM是⊙O的切線;
(2)若∠D = 60°,AD = 2,射線CO與AM交于N點,請寫出求ON長的思路.
【答案】證明見解析
【解析】試題分析:(1)根據垂徑定理得到AB垂直平分CD,根據線段垂直平分線的性質得到AC=AD,得到∠BAD=![]() ∠CAD,由AM是△ACD的外角∠DAF的平分線,得到∠DAM=
∠CAD,由AM是△ACD的外角∠DAF的平分線,得到∠DAM=![]() ∠FAD,再由∠BAD與∠FAD互補,得出∠BAM=90°,根據切線的判定即可得到結論;
∠FAD,再由∠BAD與∠FAD互補,得出∠BAM=90°,根據切線的判定即可得到結論;
(2)根據有一個角是60°的等腰三角形是等邊三角形推出△ACD是等邊三角形,得到CD=AD=2,再根據等邊三角形的性質和三角形的內角和定理求出∠5=∠4=30°,AN=AC=2,利用三角函數解直角三角形即可得到結論.
試題解析:
(1)證明:∵AB⊥CD,AB是⊙O的直徑,
∴![]() .
.
∴![]() .
.
∵AM是∠DAF的角平分線,
∴![]() .
.
∵![]() °,
°,
∴![]() °.
°.
∴OA⊥AM.
∴AM是⊙O的切線.
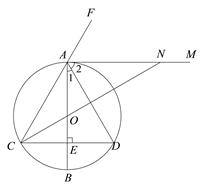
(2)思路:①由AB⊥CD,AB是⊙O的直徑,可得AC=AD,∠1=∠3=![]() ∠CAD;
∠CAD;
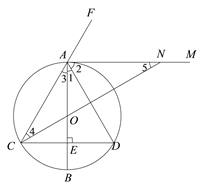
②由∠D=60°,AD=2,可得△ACD為邊長為2的等邊三角形,∠1=∠3=30°;
③由OA=OC,可得∠4=∠3=30°;
④由∠CAN=∠3+∠BAN=30°+90°=120°,可得∠5=∠4=30°,AN=AC=2;
⑤在Rt△OAN中,根據三角函數即可求出ON的長.


科目:初中數學 來源: 題型:
【題目】若A、B、C為數軸上三點,若點C到A的距離是點C到B的距離2倍,我們就稱點C是(A,B)的好點.例如,如圖1,點A表示的數為﹣1,點B表示的數為2.表示1的點C到點A的距離是2,到點B的距離是1,那么點C是(A,B)的好點;又如,表示0的點D到點A的距離是1,到點B的距離是2,那么點D就不是(A,B)的好點,但點D是(B,A)的好點.

知識運用:如圖2,M、N為數軸上兩點,點M所表示的數為﹣2,點N所表示的數為4.

(1)數 所表示的點是(M,N)的好點;
(2)如圖3,A、B為數軸上兩點,點A所表示的數為﹣20,點B所表示的數為40.現有一只電子螞蟻P從點B出發,以2個單位每秒的速度向左運動,到達點A停止.當t為何值時,P、A和B中恰有一個點為其余兩點的好點?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC是等邊三角形,△ADC與△ABC關于直線AC對稱,AE與CD垂直交BC的延長線于點E,∠EAF=45°,且AF與AB在AE的兩側,EF⊥AF.
(1)依題意補全圖形.
(2)①在AE上找一點P,使點P到點B,點C的距離和最短;
②求證:點D到AF,EF的距離相等.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】把下列各數分別填入相應的集合里:0,-3.14,-(-10),![]() ,-4
,-4![]() ,15%,
,15%,![]() ,0.3,
,0.3,![]() ,10.01001000100001…
,10.01001000100001…
非負整數集合:{ …}
正分數集合:{ …}
無理數集合:{ …}
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀第①小題的計算方法,再計算第②小題.
①–5![]() +(–9
+(–9![]() )+17
)+17![]() +(–3
+(–3![]() )
)
解:原式=[(–5)+(–![]() )]+[(–9)+(–
)]+[(–9)+(–![]() )]+(17+
)]+(17+![]() )+[(–3+(–
)+[(–3+(–![]() )]
)]
=[(–5)+(–9)+(–3)+17]+[(–![]() )+(–
)+(–![]() )+(–
)+(–![]() )+
)+![]() ]
]
=0+(–1![]() )
)
=–1![]() .
.
上述這種方法叫做拆項法.靈活運用加法的交換律、結合律可使運算簡便.
②仿照上面的方法計算:(﹣2000![]() )+(﹣1999
)+(﹣1999![]() )+4000
)+4000![]() +(﹣1
+(﹣1![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】菱形ABCD的周長為24,∠ABC=60°,以AB為腰在菱形外作底角為45°的等腰△ABE,連結AC,CE,則△ACE的面積為___________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知數軸上點A表示的數為8,B是數軸上位于點A左側一點,且AB=20,
(1)寫出數軸上點B表示的數 ;
(2)|5﹣3|表示5與3之差的絕對值,實際上也可理解為5與3兩數在數軸上所對的兩點之間的距離.如|x﹣3|的幾何意義是數軸上表示有理數x的點與表示有理數3的點之間的距離.試探索:
①:若|x﹣8|=2,則x= .
②:|x+12|+|x﹣8|的最小值為 .
(3)動點P從O點出發,以每秒5個單位長度的速度沿數軸向右勻速運動,設運動時間為t(t>0)秒.求當t為多少秒時?A,P兩點之間的距離為2;
(4)動點P,Q分別從O,B兩點,同時出發,點P以每秒5個單位長度沿數軸向右勻速運動,Q點以P點速度的兩倍,沿數軸向右勻速運動,設運動時間為t(t>0)秒.問當t為多少秒時?P,Q之間的距離為4.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
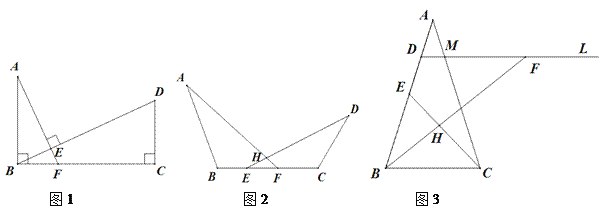
【題目】(1)【特殊發現】如圖1,AB⊥BC于B,CD⊥BC于C,連接BD,過A作AF⊥BD,交BD于E,交BC于F,若BF=1,BC=3,則AB·CD= ;
(2)【類比探究】如圖2,在線段BC上存在點E,F,連接AF,DE交于點H,若∠ABC=∠AHD=∠ECD,求證:AB·CD=BF·CE;
(3)【解決問題】如圖3,在等腰△ABC中,AB=AC=4,E為AB中點,D為AE中點,過點D作直線DM∥BC,在直線DM上取一點F,連接BF交CE于點H,使∠FHC=∠ABC,問:DF·BC是否為定值?若是,請求出,若不是,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
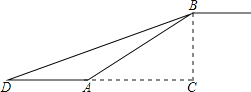
【題目】如圖,在合肥地鐵3號線某站通道的建設中,建設工人將坡長為20米![]() 米
米![]() 、坡角為
、坡角為![]() 的斜坡通道改造成坡角為
的斜坡通道改造成坡角為![]() 的斜坡通道,使斜坡的起點從點A處向左平移至點D處,求改造后的斜坡通道BD的長
的斜坡通道,使斜坡的起點從點A處向左平移至點D處,求改造后的斜坡通道BD的長![]() 結果精確到
結果精確到![]() 米
米![]() 參考數據:
參考數據: ![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com