
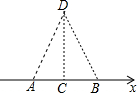
 如圖,長為12cm的彈性皮筋直放置在x軸上,固定兩端A和B,然后把中點C向上拉升8cm至D點,則彈性皮筋被拉長了8cm.
如圖,長為12cm的彈性皮筋直放置在x軸上,固定兩端A和B,然后把中點C向上拉升8cm至D點,則彈性皮筋被拉長了8cm. 分析 根據勾股定理,可求出AD、BD的長,則AD+BD-AB即為橡皮筋拉長的距離.
解答 解:根據題意得:AD=BD,AC=BC,AB⊥CD,
則在Rt△ACD中,AC=$\frac{1}{2}$AB=6cm,CD=8cm;
根據勾股定理,得:AD=$\sqrt{A{C}^{2}+C{D}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10(cm);
所以AD+BD-AB=2AD-AB=20-12=8(cm);
即橡皮筋被拉長了8cm;
故答案為:8cm.
點評 此題主要考查了等腰三角形的性質以及勾股定理的應用;熟練掌握等腰三角形的性質,由勾股定理求出AD是解決問題的關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源:2016-2017學年河南省七年級下學期第一次月考(3月)數學試卷(解析版) 題型:單選題
如圖,已知AB∥CD,∠C=70°,∠F=30°,則∠A的度數為( )

A. 30° B. 35° C. 40°  D. 45°
D. 45°
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com