
【題目】(1)問題發現
如圖1,△ACB和△DCE均為等邊三角形,點A,D,E在同一直線上,連接BE,求∠AEB的度數.
(2)拓展探究
如圖2,△ACB和△DCE均為等腰直角三角形,∠ACB=∠DCE=90°,點A、D、E在同一直線上,CM為△DCE中DE邊上的高,連接BE.請求∠AEB的度數及線段CM,AE,BE之間的數量關系,并說明理由.

【答案】(1)60°;(2)∠AEB=90°AE= BE+2CM.
【解析】解:(1)∵△ACB和△DCE均為等邊三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=60°,
∴∠ACD=60°﹣∠DCB =∠BCE.
在△ACD和△BCE中,
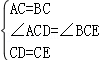 ,
,
∴△ACD≌△BCE(SAS).
∴∠ADC=∠BEC.
∵△DCE為等邊三角形,
∴∠CDE=∠CED=60°.
∵點A,D,E在同一直線上,
∴∠ADC=120°,
∴∠BEC=120°.
∴∠AEB=∠BEC﹣∠CED=60°.
(2)
∵△ACB和△DCE均為等腰直角三角形,∠ACB=∠DCE=90°
∴CA=CB,CD=CE.
且∠ACD=∠BCE.
在△ACD和△BCE中,
 ,
,
∴△ACD≌△BCE(SAS).
∴AD=BE,∠ADC=∠BEC.
∵△DCE為等腰直角三角形,
∴∠CDE=∠CED=45°.
∵點A,D,E在同一直線上,
∴∠ADC=135°,
∴∠BEC=135°.
∴∠AEB=∠BEC﹣∠CED=90°.
∵CD=CE,CM⊥DE,
∴DM=ME.
∵∠DCE=90°,
∴DM=ME=CM.
∴AE=AD+DE=BE+2CM.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】如圖,已知點A是一次函數![]() (x≥0)圖象上一點,過點A作x軸的垂線l,B是l上一點(B在A上方),在AB的右側以AB為斜邊作等腰直角三角形ABC,反比例函數
(x≥0)圖象上一點,過點A作x軸的垂線l,B是l上一點(B在A上方),在AB的右側以AB為斜邊作等腰直角三角形ABC,反比例函數![]() (x>0)的圖象過點B,C,若△OAB的面積為6,則△ABC的面積是______.
(x>0)的圖象過點B,C,若△OAB的面積為6,則△ABC的面積是______.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm, BC=26cm.,點P從點A出發,以1cm/s的速度向點D運動;點Q從點C同時出發,以3cm/s的速度向點B運動。規定其中一個動點到達端點時,另一個動點也隨之停止運動。從運動開始,使PQ=CD,需要經過多長時間?
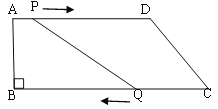
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某日孫老師佩戴運動手環進行快走鍛煉,兩次鍛煉后數據如下表.與第一次鍛煉相比,孫老師第二次鍛煉步數增長的百分率是其平均步長減少的百分率的3倍.根據經驗已知孫老師第二次鍛煉時平均步長減少的百分率小于0.5.
項目 | 第一次鍛煉 | 第二次鍛煉 | ||
步數(步) | 10000 | ① | ||
平均步長(米/步) | 0.6 | ② | ||
距離(米) | 6000 | 7020 |
注:步數×平均步長=距離.
(1)求孫老師第二次鍛煉時平均步長減少的百分率;
(2)孫老師發現好友中步數排名第一為24000步,因此在兩次鍛煉結束后又走了500米,使得總步數恰好為24000步,求孫老師這500米的平均步長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列調查活動中適合用全面調查的是( )
A.“奔跑吧,兄弟”節目的收視率
B.調查乘坐飛機的旅客是否帶了違禁物品
C.某種品牌節能燈的使用壽命
D.了解河北省中學生課外閱讀的情況
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列材料:
問題:已知方程x2+x﹣1=0,求一個一元二次方程,使它的根分別是已知方程根的2倍.
解:設所求方程的根為y,則y=2x,所以x=![]() ,把x=
,把x=![]() ,代入已知方程,
,代入已知方程,
得(![]() )2 +
)2 +![]() ﹣1=0.
﹣1=0.
化簡,得y2+2y﹣4=0,
故所求方程為y2+2y﹣4=0
這種利用方程根的代換求新方程的方法,我們稱為“換根法”.
請用閱讀材料提供的“換根法”求新方程(要求:把所求方程化為一般形式):
(1)已知方程x2+2x﹣1=0,求一個一元二次方程,使它的根分別是已知方程根的相反數,則所求方程為 ;
(2)已知關于x的一元二次方程ax2+bx+c=0(a≠0)有兩個不等于零的實數根,求一個一元二次方程,使它的根分別是已知方程根的倒數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com