
 交y軸于點(diǎn)A.拋物線
交y軸于點(diǎn)A.拋物線 的圖象過點(diǎn)E(-1,0),并與直線l相交于A、B兩點(diǎn).
的圖象過點(diǎn)E(-1,0),并與直線l相交于A、B兩點(diǎn).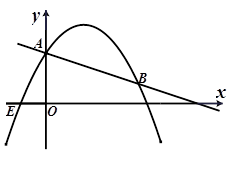
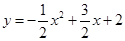
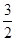 ,
,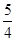 )
)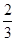 ,0),M2(
,0),M2(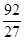 ,0),M3(
,0),M3(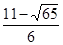 ,0),M4(
,0),M4(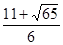 ,0)
,0) 交y軸于點(diǎn)A(0,2),
交y軸于點(diǎn)A(0,2), 上的點(diǎn),
上的點(diǎn),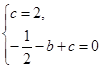 ,解得
,解得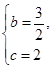 .
.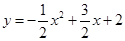 .
. 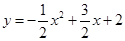 =
=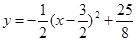 ,∴對(duì)稱軸為x=
,∴對(duì)稱軸為x=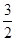 ,
,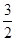 的對(duì)稱點(diǎn)為F(4,0).
的對(duì)稱點(diǎn)為F(4,0).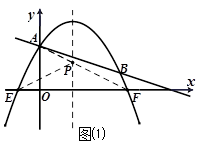
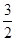 的交點(diǎn)即為所求P點(diǎn),由于E、F兩點(diǎn)關(guān)于對(duì)稱軸對(duì)稱,則此時(shí)△PAE的周長(zhǎng)=PA+PE+AE
的交點(diǎn)即為所求P點(diǎn),由于E、F兩點(diǎn)關(guān)于對(duì)稱軸對(duì)稱,則此時(shí)△PAE的周長(zhǎng)=PA+PE+AE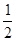 ,
,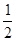 x+2.
x+2.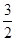 時(shí),y=
時(shí),y=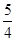 ,∴P點(diǎn)坐標(biāo)為(
,∴P點(diǎn)坐標(biāo)為(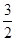 ,
,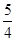 ).
). 交x軸于點(diǎn)C,令y=0,得x=6,∴C(6,0).
交x軸于點(diǎn)C,令y=0,得x=6,∴C(6,0).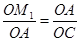 .
.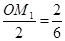 ,
,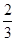 ,∴M1(-
,∴M1(-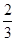 ,0).
,0). 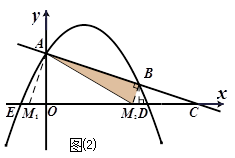
 和拋物線
和拋物線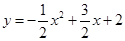 的交點(diǎn),
的交點(diǎn),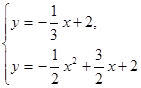 ,解得
,解得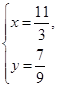 ,或
,或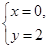 (舍)
(舍)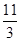 ,
,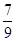 ).
).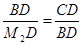 .
.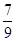 ,M2D=
,M2D=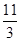 -m,CD=6-
-m,CD=6-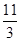 =
=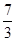 ,
,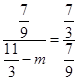 ,解得m=
,解得m=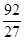 ,∴M2(
,∴M2(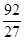 ,0).
,0).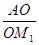 =3,
=3,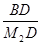 =
=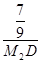 =3,
=3,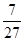 .∴OM2=OD-M2D=
.∴OM2=OD-M2D=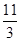 -
-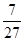 =
=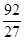 ,
, ,0).
,0).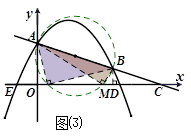
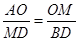 .
.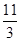 -t,OM=t,BD=
-t,OM=t,BD=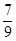 ,
,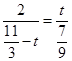 ,解得
,解得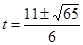 ,
,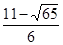 ,0),M4(
,0),M4(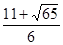 ,0).
,0).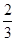 ,0),M2(
,0),M2(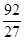 ,0),M3(
,0),M3(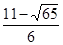 ,0),M4(
,0),M4(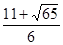 ,0).
,0).

 名題金卷系列答案
名題金卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源:不詳 題型:解答題
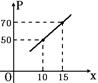
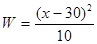 .在推廣20cm~40cm的隔熱瓦時(shí),廠家進(jìn)行市場(chǎng)營(yíng)銷,這種規(guī)格的隔熱瓦廣告費(fèi)為每片10元.要使每片隔熱瓦的利潤(rùn)不低于60.4元,求5cm~60cm的隔熱瓦邊長(zhǎng)x的取值范圍(x取整數(shù)).
.在推廣20cm~40cm的隔熱瓦時(shí),廠家進(jìn)行市場(chǎng)營(yíng)銷,這種規(guī)格的隔熱瓦廣告費(fèi)為每片10元.要使每片隔熱瓦的利潤(rùn)不低于60.4元,求5cm~60cm的隔熱瓦邊長(zhǎng)x的取值范圍(x取整數(shù)).查看答案和解析>>
科目:初中數(shù)學(xué) 來源:不詳 題型:單選題

A.y=- x2+x x2+x | B.y=-x2+x | C.y=- x2-x x2-x | D.y= x2-x x2-x |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源:不詳 題型:填空題
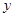 軸,且在
軸,且在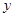 軸的左側(cè)部分是上升的,那么這個(gè)拋物線表達(dá)式可以是 .
軸的左側(cè)部分是上升的,那么這個(gè)拋物線表達(dá)式可以是 .查看答案和解析>>
科目:初中數(shù)學(xué) 來源:不詳 題型:單選題
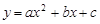 的圖象與x軸交于(
的圖象與x軸交于(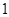 ,0)和(
,0)和(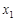 ,0),其中
,0),其中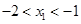 ,與
,與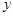 軸交于正半軸上一點(diǎn).下列結(jié)論:①
軸交于正半軸上一點(diǎn).下列結(jié)論:①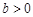 ;②
;②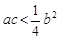 ;③
;③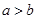 ;④
;④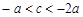 .其中所有正確結(jié)論的序號(hào)是_______.
.其中所有正確結(jié)論的序號(hào)是_______.查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com