
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 首先根據線段的中垂線上的點到線段兩端點的距離相等,求出AB的中垂線與x軸的交點,即可求出點C1的坐標;然后再求出AB的長,以點A為圓心,以AB的長為半徑畫弧,與x軸的交點為點C2、C3;最后判斷出以點B為圓心,以AB的長為半徑畫弧,與x軸沒有交點,據此判斷出點C的個數為多少即可.
解答 解:如圖,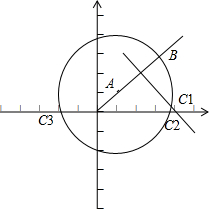
∵AB所在的直線是y=x,
∴設AB的中垂線所在的直線是y=-x+b,
∵點A(1,1),B(3,3),
∴AB的中點坐標是(2,2),
把x=2,y=2代入y=-x+b,
解得b=4,
∴AB的中垂線所在的直線是y=-x+4,
∴C1(4,0)
以點A為圓心,以AB的長為半徑畫弧,與x軸的交點為點C2、C3;
AB=$\sqrt{(3-1)^{2}+(3-1)^{2}}$=2$\sqrt{2}$,
∵2$\sqrt{2}$<3,
∴以點B為圓心,以AB的長為半徑畫弧,與x軸沒有交點.
綜上,可得若以A、B、C三點為頂點的三角形是等腰三角形,則點C的個數為3.
故選:B.
點評 此題主要考查了等腰三角形的性質和應用,考查了分類討論思想的應用,要熟練掌握,解答此題的關鍵是要明確:①等腰三角形的兩腰相等.②等腰三角形的兩個底角相等.③等腰三角形的頂角平分線、底邊上的中線、底邊上的高相互重合.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
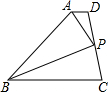 如圖,已知四邊形ABCD中,AD∥BC,AP平分∠DAB,BP平分∠ABC,它們的交點P給在線段CD上,下面的結論:①AP⊥BP;②點P到直線AD、BC的距離相等;③PD=PC.其中正確的結論有( )
如圖,已知四邊形ABCD中,AD∥BC,AP平分∠DAB,BP平分∠ABC,它們的交點P給在線段CD上,下面的結論:①AP⊥BP;②點P到直線AD、BC的距離相等;③PD=PC.其中正確的結論有( )| A. | ①②③ | B. | ①② | C. | 僅① | D. | 僅② |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com