
【題目】某件商品的成本價為15元,據市場調查得知,每天的銷量y(件)與價格x(元)有下列關系:
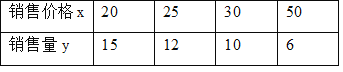
(1)根據表中數據,在直角坐標系中描出實數對(x,y)的對應點,并畫出圖象;
(2)猜測確定y與x間的關系式.
(3)設總利潤為W元,試求出W與x之間的函數關系式,若售價不超過30元,求出當日的銷售單價定為多少時,才能獲得最大利潤?
【答案】(1)畫圖見解析;(2)(2)![]() ;(3)當
;(3)當![]() 時,
時, ![]()
【解析】(1)根據描點法作函數的圖象,先描點,連線即可得到答案,
(2)觀察表中數據可得,x與y的積為常數,判斷為反比例函數,根據數據,易得k的值,進而可得函數關系式,
(3)根據題意,易得關系式,根據反比例函數的單調性分析可得答案.
解:(1)根據描點法作函數的圖象,先描點,連線即可得圖象,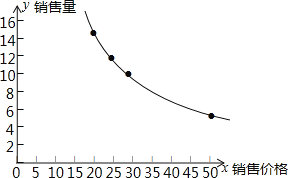
(2)觀察表中數據可得,x與y得積為常數,判斷為反比例函數,
根據數據,易得K=20×15=300,
故其解析式為y=![]() .
.
(3)w=(x-15) ![]() =300-
=300-![]() ;
;
當x≤30時,因為w隨x增大而增大,
∴當x=30時,w最大=150.
“點睛”主要考查了函數的應用.解題的關鍵是根據實際意義列出函數關系式,從實際意義中找到對應的變量的值,利用待定系數法求出函數解析式,再根據自變量的值求算對應的函數值.本題尤其要注意分兩種情況考慮,然后根據數據的規律舍去一種情況.


科目:初中數學 來源: 題型:
【題目】如圖,某小區內有一塊長、寬比為2∶1的矩形空地,計劃在該空地上修筑兩條寬均為2 m的互相垂直的小路,余下的四塊小矩形空地鋪成草坪,如果四塊草坪的面積之和為312 m2,請求出原來大矩形空地的長和寬.
(1)請找出上述問題中的等量關系:_________________;
(2)若設大矩形空地的寬為xm,可列出的方程為_____________,方程的解為__________,原來大矩形空地的長和寬分別為_________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,長方形ABCD的各邊與坐標軸都平行,點A,C的坐標分別為(-1,1),(![]() ,-2
,-2![]() ).
).
(1)求點B,D的坐標.
(2)一動點P從點A出發,沿長方形的邊AB,BC運動至點C停止,運動速度為每秒![]() 個單位長度,設運動時間為t s.
個單位長度,設運動時間為t s.
①當t=1時,求點P的坐標;
②當t=3時,求三角形PDC的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
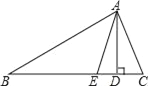
【題目】已知,如圖,在△ABC中,AD,AE分別是△ABC的高和角平分線,若∠ABC=30°,∠ACB=50°.
(1)求∠DAE的度數;
(2)寫出∠DAE與∠ACB﹣∠ABC的數量關系: ,并證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市公交快速通道開通后,為響應市政府“綠色出行”的號召,家住新城的小王上班由自駕車改為乘坐公交車.已知小王家距上班地點18千米,他用乘公交車的方式平均每小時行駛的路程比他用自駕車的方式平均每小時行駛的路程的2倍還多9千米,他從家出發到達上班地點,乘公交車方式所用時間是自駕車方式所用時間的![]() .小王用自駕車方式上班平均每小時行駛多少千米?
.小王用自駕車方式上班平均每小時行駛多少千米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為積極響應南充市創建“全國衛生城市”的號召,某校1 500名學生參加了衛生知識競賽,成績記為A、B、C、D四等。從中隨機抽取了部分學生成績進行統計,繪制成如下兩幅不完整的統計圖表,根據圖表信息,以下說法不正確的是( )
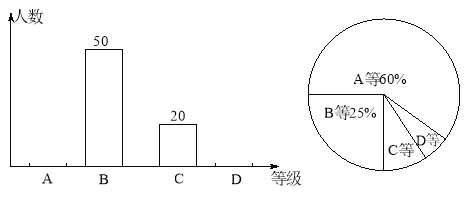
A.樣本容量是200
B.D等所在扇形的圓心角為15°
C.樣本中C等所占百分比是10%
D.估計全校學生成績為A等大約有900人
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】4月23日是“世界讀書日”,學校開展“讓書香溢滿校園”讀書活動,以提升青少年的閱讀興趣,九年級(1)班數學活動小組對本年級600名學生每天閱讀時間進行了統計,根據所得數據繪制了如圖所示的兩幅不完整的統計圖(每組包括最小值不包括最大值)九年級(1)班每天閱讀時間在0.5 h以內的學生占全班人數的8%,根據統計圖解答下列問題: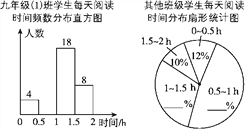
(1)九年級(1)班有________名學生.
(2)補全頻數分布直方圖.
(3)除九年級(1)班外,九年級其他班級每天閱讀時間為1~1.5 h的學生有165人,請你補全扇形統計圖.
(4)求該年級每天閱讀時間不少于1 h的學生有多少人.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,已知點A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2),把一根長為2017個單位長度且沒有彈性的細線(線的粗細忽略不計)的一端固定在A處,并按A→B→C→D→A…的規律緊繞在四邊形ABCD的邊上,則細線的另一端所在位置的點的坐標是( )
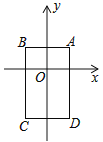
A. (﹣1,﹣2) B. (―1,1)
C. (-1,-1) D. (1,―2)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若∠C=α,∠EAC+∠FBC=β
(1)如圖①,AM是∠EAC的平分線,BN是∠FBC的平分線,若AM∥BN,則α與β有何關系?并說明理由.
(2)如圖②,若∠EAC的平分線所在直線與∠FBC平分線所在直線交于P,試探究∠APB與α、β的關系是______.(用α、β表示)
(3)如圖③,若α≥β,∠EAC與∠FBC的平分線相交于P1,∠EAP1與∠FBP1的平分線交于P2 ;依此類推,則∠P5=______.(用α、β表示)



查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com