Question

7．如圖，OC平分∠AOB，∠AOB=90°，點P是射線OC上一點，且OP=4，點M、N分別在射線OA和射線OB上，若△PMN是等腰直角三角形，則符合條件的△PMN有無數個．

Answer 1

分析 先作出特殊位置的圖1，再作圖2：先作等腰△PMN，證明后發現，△PMN也是等腰直角三角形．

解答 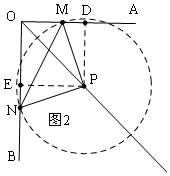解：①如圖1，當PM⊥OA，PN⊥OB時，△PMN是等腰直角三角形；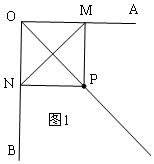

②如圖2，在OA上任意取一點M，連接PM，以P為圓心，PM為半徑作圓，交射線OB于N，連接MN、PN，則△PMN是等腰直角三角形；
理由是：過P分別作OA、OB的垂線段PD、PE，垂足分別為D、E，
則∠PDM=∠PEN=90°，
∵OC平分∠AOB，
∴PD=PE，
∵PM=PN，
∴Rt△PDM≌Rt△PEN，
∴∠DPM=∠EPN，
∵∠EPD=90°，
∴∠MPN=90°，
∴△PMN是等腰直角三角形，
綜上所述，符合條件的△PMN有無數個；
故答案為：無數．

點評 本題考查了全等三角形、等腰直角三角形的性質和判定、角平分線的性質，明確等腰直角三角形的兩直角邊相等，兩銳角都是45°；并運用全等三角形確定所畫的等腰三角形是等腰直角三角形．