Question

關于x的方程2x²+（m²-9）x+m+1=0，當m=      時，兩根互為倒數．

Answer 1

【答案】分析：設方程的兩根為x₁，x₂，根據根與系數的關系得到x₁+x₂=-=0，解得m₁=3，m₂=-3，然后把m的值分別代入方程，運用根的判別式確定滿足條件的m的值．
解答：解：設方程的兩根為x₁，x₂，則x₁+x₂=-=0，解得m₁=3，m₂=-3，
當m=3時，原方程化為2x²+4=0，此方程無解，故舍去；
當m=-3時，原方程化為2x²-2=0，此方程有解，
所以m=-3．
故答案為：-3．
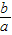
點評：本題考查了一元二次方程ax²+bx+c=0（a≠0）的根與系數的關系：若方程的兩根為x₁，x₂，則x₁+x₂=-，x₁•x₂=．也考查了一元二次方程的根的判別式．