

分析 (1)連接BF,過D作DM⊥BF,過E作EN⊥BF于N,于是得到MN=DE=25cm,EN=DM,根據平行線的性質得到∠F=∠ODE=60°,∠B=∠OED=50°,求得EN=DM=20$\sqrt{3}$=34.6,MF=20,由三角函數的定義得到BN=$\frac{EN}{tan50°}$=$\frac{20\sqrt{3}}{1.19}$≈29.08,于是得到結論;
(2)根據三角函數的定義即刻得到結論.
解答 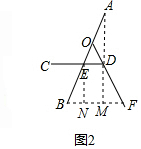 解:(1)連接BF,過D作DM⊥BF,過E作EN⊥BF于N,
解:(1)連接BF,過D作DM⊥BF,過E作EN⊥BF于N,
則MN=DE=25cm,EN=DM,
∵DE∥BF,
∴∠F=∠ODE=60°,∠B=∠OED=50°,
∵DF=40,
∴EN=DM=20$\sqrt{3}$=34.6,MF=20,
∴BN=$\frac{EN}{tan50°}$=$\frac{20\sqrt{3}}{1.19}$≈29.08,
∴BF=BN+MN+MF=74.08cm,
故兩支架著地點B,F之間的距離我74.08cm;
(2)在Rt△ADE中,AD=DE•tan50°=29.75cm,
∴AM=29.75+20$\sqrt{3}$≈64cm,
故椅子的高度是64cm.
點評 題主要考查解直角三角形的應用,解直角三角形的一般過程是:①將實際問題抽象為數學問題(畫出平面圖形,構造出直角三角形轉化為解直角三角形問題).②根據題目已知特點選用適當銳角三角函數或邊角關系去解直角三角形,得到數學問題的答案,再轉化得到實際問題的答案.


 金鑰匙試卷系列答案
金鑰匙試卷系列答案科目:初中數學 來源: 題型:選擇題
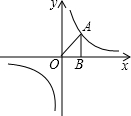 如圖,A為反比例函數y=$\frac{k}{x}$圖象上一點,AB垂直x軸于B點,若S△AOB=3,則k的值為( )
如圖,A為反比例函數y=$\frac{k}{x}$圖象上一點,AB垂直x軸于B點,若S△AOB=3,則k的值為( )| A. | 6 | B. | 3 | C. | $\frac{3}{2}$ | D. | 不能確定 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
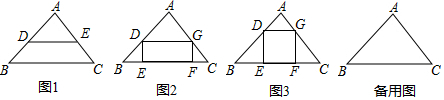
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | -$\sqrt{2}$ | B. | -$\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
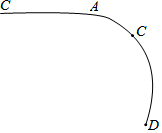 如圖,一段圓弧AB上有一個點D,直線AC與圓弧相切于點A,請借助于切點A及B、D兩點,利用尺規作圖找出這段圓弧所在圓的圓心(不寫作法,保留作圖痕跡).
如圖,一段圓弧AB上有一個點D,直線AC與圓弧相切于點A,請借助于切點A及B、D兩點,利用尺規作圖找出這段圓弧所在圓的圓心(不寫作法,保留作圖痕跡).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com