

| A. | 10° | B. | 15° | C. | 20° | D. | 25° |

| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
 如圖,河上有一座拋物線橋洞,已知橋下的水面離橋拱頂部3m時(shí),水面寬AB為6m,當(dāng)水位上升0.5m時(shí):
如圖,河上有一座拋物線橋洞,已知橋下的水面離橋拱頂部3m時(shí),水面寬AB為6m,當(dāng)水位上升0.5m時(shí):查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
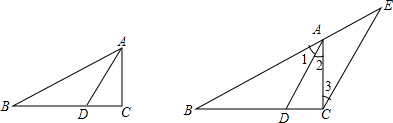
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
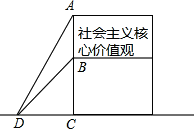 為了弘揚(yáng)“社會(huì)主義核心價(jià)值觀”,樂(lè)至縣政府在廣場(chǎng)樹立公益廣告牌,如圖所示,為固定廣告牌,在兩側(cè)加固鋼纜,已知鋼纜底端D距廣告牌立柱距離CD為3米,從D點(diǎn)測(cè)得廣告牌頂端A點(diǎn)和底端B點(diǎn)的距離分別是5米和$3\sqrt{2}$米.
為了弘揚(yáng)“社會(huì)主義核心價(jià)值觀”,樂(lè)至縣政府在廣場(chǎng)樹立公益廣告牌,如圖所示,為固定廣告牌,在兩側(cè)加固鋼纜,已知鋼纜底端D距廣告牌立柱距離CD為3米,從D點(diǎn)測(cè)得廣告牌頂端A點(diǎn)和底端B點(diǎn)的距離分別是5米和$3\sqrt{2}$米.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
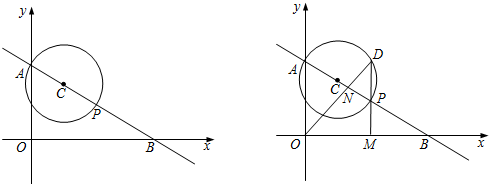
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
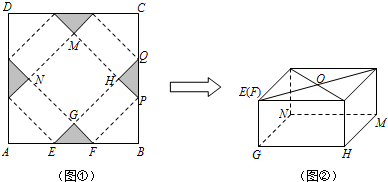
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題

查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com