
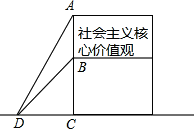
 為了弘揚“社會主義核心價值觀”,樂至縣政府在廣場樹立公益廣告牌,如圖所示,為固定廣告牌,在兩側加固鋼纜,已知鋼纜底端D距廣告牌立柱距離CD為3米,從D點測得廣告牌頂端A點和底端B點的距離分別是5米和$3\sqrt{2}$米.
為了弘揚“社會主義核心價值觀”,樂至縣政府在廣場樹立公益廣告牌,如圖所示,為固定廣告牌,在兩側加固鋼纜,已知鋼纜底端D距廣告牌立柱距離CD為3米,從D點測得廣告牌頂端A點和底端B點的距離分別是5米和$3\sqrt{2}$米.分析 (1)直接利用勾股定理得出AC的長,進而得出BC的長即可得出AB的長;
(2)利用已知結合(1)中所求得出△DBC是等腰直角三角形,進而得出答案.
解答 解:(1)在直角三角形ADC中,
AC=$\sqrt{A{{D}^{2}-DC}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4(m),
在直角三角形BDC中,
BC=$\sqrt{D{B}^{2}-D{C}^{2}}$=$\sqrt{(3\sqrt{2})^{2}-{3}^{2}}$=3(m),
故AB=AC-BC=1(米)
答:公益廣告牌的高度AB的長度為1m;
(2)∵在直角三角形BDC中,BC=CD=3m,
∴△DBC是等腰直角三角形,
∴∠BDC=45°.
點評 此題主要考查了勾股定理的應用,根據題意正確應用勾股定理是解題關鍵.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題

| A. | 10° | B. | 15° | C. | 20° | D. | 25° |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
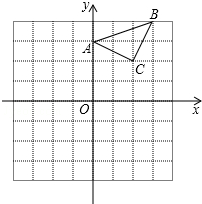 已知:△ABC在直角坐標平面內,三個頂點的坐標分別為A(0,3)、B(3,4)、C(2,2)(正方形網格中每個小正方形的邊長是一個單位長度).
已知:△ABC在直角坐標平面內,三個頂點的坐標分別為A(0,3)、B(3,4)、C(2,2)(正方形網格中每個小正方形的邊長是一個單位長度).查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
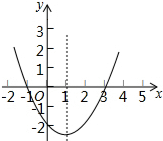 二次函數y=ax2+bx+c(a≠0)的大致圖象如圖,關于該二次函數,下列說法錯誤的是( )
二次函數y=ax2+bx+c(a≠0)的大致圖象如圖,關于該二次函數,下列說法錯誤的是( )| A. | 函數有最小值 | B. | 當-1<x<3時,y>0 | ||
| C. | 當x<1時,y隨x的增大而減小 | D. | 對稱軸是直線x=1 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com