
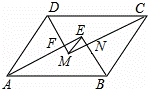
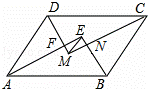
如圖,▱ABCD中,AB>AD,AE,BE,CM,DM分別為∠DAB,∠ABC,∠BCD,∠CDA的平分線,AE與DM相交于點F,BE與CM相交于點H,連接EM.若▱ABCD的周長為42cm,FM=3cm,EF=4cm,則EM= cm,AB= cm.
5. 13
解:∵AE為∠DAB的平分線,
∴∠DAE=∠EAB=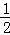 ∠DAB,
∠DAB,
同理:∠ABE=∠CBE=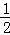 ∠ABC,
∠ABC,
∠BCM=∠DCM=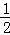 ∠BCD,
∠BCD,
∠CDM=∠ADM=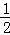 ∠ADC.
∠ADC.
∵四邊形ABCD是平行四邊形,
∴∠DAB=∠BCD,∠ABC=∠ADC,AD=BC.
∴∠DAF=∠BCN,∠ADF=∠CBN.
在△ADF和△CBN中,
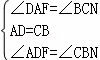 .
.
∴△ADF≌△CBN(ASA).
∴DF=BN.
∵四邊形ABCD是平行四邊形,
∴AD∥BC,
∴∠DAB+∠ABC=180°.
∴∠EAB+∠EBA=90°.
∴∠AEB=90°.
同理可得:∠AFD=∠DMC=90°.
∴∠EFM=90°.
∵FM=3,EF=4,
∴ME=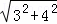 =5(cm).
=5(cm).
∵∠EFM=∠FMN=∠FEN=90°.
∴四邊形EFMN是矩形.
∴EN=FM=3.
∵∠DAF=∠EAB,∠AFD=∠AEB,
∴△AFD∽△AEB.
∴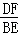 =
=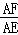 .
.
∴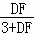 =
=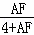 .
.
∴4DF=3AF.
設DF=3k,則AF=4k.
∵∠AFD=90°,
∴AD=5k.
∵∠AEB=90°,AE=4(k+1),BE=3(k+1),
∴AB=5(k+1).
∵2(AB+AD)=42,
∴AB+AD=21.
∴5(k+1)+5k=21.
∴k=1.6.
∴AB=13(cm).
故答案為:5、13.


科目:初中數學 來源: 題型:
為了打造區域中心城市,實現攀枝花跨越式發展,我市花城新區建設正按投資計劃有序推進.花城新區建設工程部,因道路建設需要開挖土石方,計劃每小時挖掘土石方540m3,現決定向某大型機械租賃公司租用甲、乙兩種型號的挖掘機來完成這項工作,租賃公司提供的挖掘機有關信息如表:
|
| 租金(單位:元/臺•時) | 挖掘土石方量(單位:m3/臺•時) |
| 甲型挖掘機 | 100 | 60 |
| 乙型挖掘機 | 120 | 80 |
(1)若租用甲、乙兩種型號的挖掘機共8臺,恰好完成每小時的挖掘量,則甲、乙兩種型號的挖掘機各需多少臺?
(2)如果每小時支付的租金不超過850元,又恰好完成每小時的挖掘量,那么共有幾種不同的租用方案?
查看答案和解析>>
科目:初中數學 來源: 題型:
在邊長為正整數的△ABC中,AB=AC,且AB邊上的中線CD將△ABC的周長分為1:2的兩部分,則△ABC面積的最小值為( )
A. 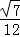 B.
B. 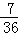
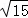 C.
C. 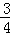
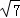 D.
D. 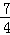
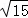
查看答案和解析>>
科目:初中數學 來源: 題型:
某公司今年銷售一種產品,1月份獲得利潤20萬元,由于產品暢銷,利潤逐月增加,3月份的利潤比2月份的利潤增加4.8萬元,假設該產品利潤每月的增長率相同,求這個增長率.
查看答案和解析>>
科目:初中數學 來源: 題型:
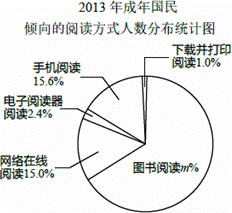
根據某研究院公布的2009~2013年我國成年國民閱讀調查報告的部分相關數據,繪制的統計圖表如下:
| 2009~2013年成年國民 年人均閱讀圖書數量統計表 | |
| 年份 | 年人均閱讀圖書數量(本) |
| 2009 | 3.88 |
| 2010 | 4.12 |
| 2011 | 4.35 |
| 2012 | 4.56 |
| 2013 | 4.78 |
根據以上信息解答下列問題:
(1)直接寫出扇形統計圖中m的值;
(2)從2009到2013年,成年國民年人均閱讀圖書的數量每年增長的幅度近似相等,估算2014年成年國民年人均閱讀圖書的數量約為 5 本;
(3)2013年某小區傾向圖書閱讀的成年國民有990人,若該小區2014年與2013年成年國民的人數基本持平,估算2014年該小區成年國民閱讀圖書的總數量約為 7500 本.
查看答案和解析>>
科目:初中數學 來源: 題型:
某茶廠用甲、乙兩臺分裝機分裝某種茶葉(每袋茶葉的標準質量為200g).為了監控分裝質量,該廠從它們各自分裝的茶葉中隨機抽取了50袋,測得它們的實際質量分析如下:
|
| 平均數(g) | 方差 |
| 甲分裝機 | 200 | 16.23 |
| 乙分裝機 | 200 | 5.84 |
則這兩臺分裝機中,分裝的茶葉質量更穩定的是 (填“甲”或“乙”).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com