
(10分)在平面直角坐標系中,如圖所示,△ABC是邊長為2的等邊三角形,將△ABC繞著點B按順時針方向旋轉得到△EDB,使得點E落在 軸的正半軸上,連結CE、AD、
軸的正半軸上,連結CE、AD、
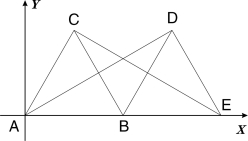
(1)求證:AD=CE;
(2)求AD的長;
(3)求過C、E兩點的直線的解析式.
(1)見解析;(2)AD=2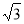 ;(3)
;(3)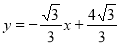
【解析】
試題分析:(1)根據旋轉圖形可得:AB=BC,BD=BE,∠ABD=∠CBE=120°得出△ABD和△CBE全等,得出所求的結論;(2)作DF⊥AE交x軸于點F,則F為BE的中點,根據Rt△BDF的勾股定理求出DF的長度,根據Rt△ADF的勾股定理求出AD的長度;(3)作CG⊥AB交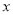 軸于點G,則G為AB的中點,求出AG和CG的長度得出點C的坐標,根據AE=BB+BE求出點E的坐標,然后利用待定系數法求出函數解析式.
軸于點G,則G為AB的中點,求出AG和CG的長度得出點C的坐標,根據AE=BB+BE求出點E的坐標,然后利用待定系數法求出函數解析式.
試題解析:(1)∵△ABC是邊長為2的等邊三角形,∴AC=AB=BC=2,∠ACB=∠CBA=∠BAC=60°
又△DBE是由△ABC繞著點B按順時針方向旋轉得到的,∴△DBE也是邊長為2的等邊三角形,
∴∠DBC=180°-60°-60°=60°,AB=BC,BD=BE又∠ABD =∠CBE=120°
∴△ABD≌△CBE(SAS) ∴AD=CE(全等三角形的對應邊相等)
(2)作DF⊥AE交x軸于點F,則F為BE的中點,∴BF=1
在Rt△BDF中,BD=2,BF=1,由勾股定理得:DF2=BD2-BF2=4-1=3,∴DF=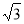
在Rt△ADF中,AF=AB+BF=2+1=3, 由勾股定理得:AD2=AF2+DF2=9+3=12, ∴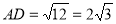
(3)作CG⊥AB交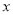 軸于點G,則G為AB的中點,∴AG=1,CG=DF=
軸于點G,則G為AB的中點,∴AG=1,CG=DF=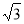
∴C點的坐標是(1, 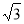 ),又AE=AB+BE=2+2=4, 故E點的坐標是(4,0)
),又AE=AB+BE=2+2=4, 故E點的坐標是(4,0)
設過C、E兩點的直線的解析式為y=kx+b,將C,E點的坐標代入解得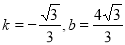 ,
,
∴過C、E兩點的直線的解析式為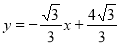
考點:三角形全等的判定與應用、待定系數法求函數解析式.


 中考解讀考點精練系列答案
中考解讀考點精練系列答案科目:初中數學 來源:2014-2015學年江蘇省啟東市九年級上學期第二次雙周測試數學試卷(解析版) 題型:解答題
如圖,⊙O與 的斜邊AB相切于點D,與直角邊AC相交于E、F兩點,連結DE,已知
的斜邊AB相切于點D,與直角邊AC相交于E、F兩點,連結DE,已知 ,⊙O的半徑為12,弧DE的長度為
,⊙O的半徑為12,弧DE的長度為 .
.

(1)求證:DE∥BC;
(2)若AF=CE,求線段BC的長度.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省東臺市九年級上學期第二次月檢測數學試卷(解析版) 題型:選擇題
如圖,在平面直角坐標系中,過格點 ,
, ,
, 作一圓弧,點
作一圓弧,點 與下列格點的連線中,能夠與該圓弧相切的是( ).
與下列格點的連線中,能夠與該圓弧相切的是( ).

A.點 B.點
B.點 C.點
C.點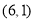 D.點
D.點
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省常熟市九年級上學期期中模擬數學試卷(解析版) 題型:填空題
如果二次函數y=ax2+bx+c的圖象的頂點坐標是(2,4),且直線y=x+4依次與y軸和拋物線相交于P、Q、R三點,PQ:QR=1:3,則這個二次函數解析式為 .
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省常熟市九年級上學期期中模擬數學試卷(解析版) 題型:選擇題
二次函數y=ax2+bx+c的y與x的部分對應值如下表:
x | … | 0 | 1 | 3 | 4 | … |
y | … | 2 | 4 | 2 | ﹣2 | … |
則下列判斷中正確的是( )
A.拋物線開口向上
B.拋物線與y軸交于負半軸
C.當x=﹣1時y>0
D.方程ax2+bx+c=0的負根在0與﹣1之間
查看答案和解析>>
科目:初中數學 來源:2014-2015學年湖南省婁底市九年級上學期期末考試數學試卷(解析版) 題型:解答題
(6分) 李大爺的魚塘今年放養魚苗10萬條,根據這幾年的統計分析,魚苗成活率約為95%,現準備打撈出售,第一網撈出40條,稱得平均每條魚重2.5千克,第二網撈出25條,稱得平均每條魚重2.2千克,第三網撈出35條,稱得平均每條魚重2.8千克,請你幫助李大爺估算今年魚塘中魚的總重量.如果每千克售價為4元,那么,李大爺今年的收入如何?
查看答案和解析>>
科目:初中數學 來源:2014-2015學年湖南省婁底市九年級上學期期末考試數學試卷(解析版) 題型:填空題
如圖,為估算某河的寬度,在河對岸邊選定一個目標點A,在近岸取點B,C,D,使得AB⊥BC,CD⊥BC,點E在BC上,并且點A,E,D在同一條直線上。若測得BE=45m,EC=15m,CD=10m,則河的寬度AB等于 .

查看答案和解析>>
科目:初中數學 來源:2014-2015學年湖北省容城鎮三閭學校九年級上學期期中考試數學試卷(解析版) 題型:解答題
某工廠生產的某種產品按質量分為10個檔次.第1檔次(最低檔次)的產品一天能生產76件,每件利潤10元.每提高一個檔次,每件利潤增加2元,但一天產量減少4件.
(1)若生產第x檔次的產品一天的總利潤為y元(其中x為正整數,且1≤x≤10),求出y關于x的函數關系式;
(2)若生產第x檔次的產品一天的總利潤為1080元,求該產品的質量檔次.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年福建省龍巖市九年級上學期第三次月考數學試卷(解析版) 題型:選擇題
二次函數 的最小值是( ).]
的最小值是( ).]
A.-35 B.-30 C.-5 D.20
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com