
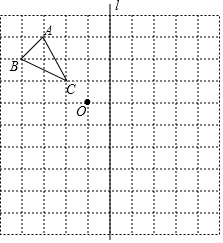
 如圖,在邊長為1個單位長度的正方形網格中,有一個格點△ABC(各個頂點都是正方形網格的格點).
如圖,在邊長為1個單位長度的正方形網格中,有一個格點△ABC(各個頂點都是正方形網格的格點).分析 (1)利用對稱的性質分別作出A、B、C關于直線l的對稱點A1、B1、C1即可得到△A1B1C1;
(2)延長AO到A2使A2O=2OA,則點A2為點A的對應點,同樣方法作出B、C的對應點B2、C2,從而得到△A2B2C2為所作;
(3)根據網格特點和旋轉的性質畫出A、B、C對稱點A3、B3、C3,從而得到△A3B3C3.
解答 解:(1)如圖,△A1B1C1為所作;
(2)如圖,△A2B2C2為所作;
(3)如圖,△A3B3C3為所作.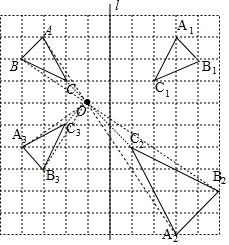
點評 本題考查了作圖-旋轉變換:根據旋轉的性質可知,對應角都相等都等于旋轉角,對應線段也相等,由此可以通過作相等的角,在角的邊上截取相等的線段的方法,找到對應點,順次連接得出旋轉后的圖形.也考查了對稱軸和旋轉變換.


 鷹派教輔銜接教材河北教育出版社系列答案
鷹派教輔銜接教材河北教育出版社系列答案科目:初中數學 來源: 題型:解答題
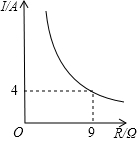 已知蓄電池的電壓U為定值,使用蓄電池時,電流I(單位:A)與電阻R(單位:Ω)是反比例函數關系,它的圖象如圖所示.
已知蓄電池的電壓U為定值,使用蓄電池時,電流I(單位:A)與電阻R(單位:Ω)是反比例函數關系,它的圖象如圖所示.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com