Question

12．實踐探究，解決問題
如圖1，△ABC中，AD為BC邊上的中線，則S_△ABD=S_△ACD．
（1）在圖2中，E、F分別為矩形ABCD的邊AD、BC的中點，且AB=4，AD=8，則S_陰影=16；
（2）在圖3中，E、F分別為平行四邊形ABCD的邊AD、BC的中點，則S_陰影和S_{平行四邊形ABCD}之間滿足的關(guān)系式為S_陰影=$\frac{1}{2}$S_{平行四邊形ABCD}之；
（3）在圖4中，E、F分別為任意四邊形ABCD的邊AD、BC的中點，則S_陰影和S_{四邊形ABCD}之間還滿足（2）中的關(guān)系式嗎？若滿足，請予以證明，若不滿足，說明理由．
解決問題：
（4）在圖5中，E、G、F、H分別為任意四邊形ABCD的邊AD、AB、BC、CD的中點，并且圖中陰影部分的面積為20平方米，求圖中四個小三角形的面積和（即S₁+S₂+S₃+S₄的值）．

Answer 1

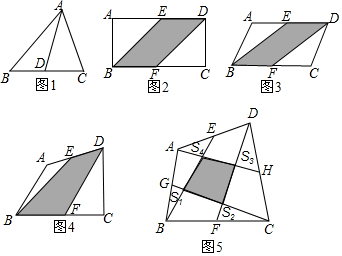
分析 （1）由矩形的性質(zhì)容易得出結(jié)果；
（2）由平行四邊形的性質(zhì)容易得出結(jié)果；
（3）連接BD，由題意得出S_△EBD=$\frac{1}{2}$ S_△ABD 同理S_△BDF=$\frac{1}{2}$S_△BDC，即可得出結(jié)論；
（4）設(shè)四邊形的空白區(qū)域分別為a，b，c，d，由（3）可以得出：a+S₂+S₃=$\frac{1}{2}$S_△ACD①，c+S₁+S₄=$\frac{1}{2}$S_△ACB②，b+S₂+S₁=$\frac{1}{2}$S_△ABD③，d+S₄+S₃=$\frac{1}{2}$S_△ACD④，進(jìn)一步得出結(jié)論即可．

解答 解：（1）∵E、F分別為矩形ABCD的邊AD、BC的中點，且AB=4，AD=8，
∴S_陰影=$\frac{1}{2}$×8×4=16，
故答案為：16；
（2）∵E、F分別為平行四邊形ABCD的邊AD、BC的中點，
∴S_陰影=$\frac{1}{2}$S_{平行四邊形ABCD}；
故答案為：S_陰影=$\frac{1}{2}$S_{平行四邊形ABCD}；
（3）滿足（2）中的關(guān)系式，理由如下：
連接BD，由圖1得S_△EBD=$\frac{1}{2}$ S_△ABD 同理S_△BDF=$\frac{1}{2}$S_△BDC
∴S_{四邊形EBFD}=S_△EBD+S_△BDF=$\frac{1}{2}$ S_{四邊形ABCD}；
（4）解：設(shè)四邊形的空白區(qū)域分別為a，b，c，d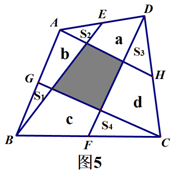
由上述性質(zhì)可以得出：
a+S₂+S₃=$\frac{1}{2}$S_△ACD①，c+S₁+S₄=$\frac{1}{2}$S_△ACB②，b+S₂+S₁=$\frac{1}{2}$S_△ABD③，d+S₄+S₃=$\frac{1}{2}$S_△ACD④，
①+②+③+④得，a+S₂+S₃+c+S₁+S₄+b+S₂+S₁+d+S₄+S₃=S_{四邊形ABCD}⑤
而S_{四邊形ABCD}=a+b+c+d+S₁+S₂+S₃+S₄+S_陰影⑥

所以聯(lián)立⑤⑥得S₁+S₂+S₃+S₄=S_陰影=20平方米．

點評 本題是三角形綜合題目，考查了矩形的性質(zhì)、平行四邊形的性質(zhì)、三角形的中線性質(zhì)等知識；本題綜合性強(qiáng)，有一定難度，熟練掌握三角形的中線性質(zhì)和平行四邊形的性質(zhì)是解決問題的關(guān)鍵．