
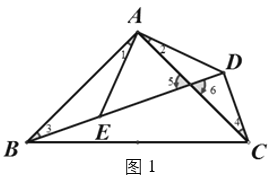
【題目】(1)如圖1,等腰![]() 和等腰
和等腰![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 三點(diǎn)在同一直線上,求證:
三點(diǎn)在同一直線上,求證:![]() ;
;
(2)如圖2,等腰![]() 中,
中,![]() ,
,![]() ,
,![]() 是三角形外一點(diǎn),且
是三角形外一點(diǎn),且![]() ,求證:
,求證:![]() ;
;
(3)如圖3,等邊![]() 中,
中,![]() 是形外一點(diǎn),且
是形外一點(diǎn),且![]() ,
,
①![]() 的度數(shù)為 ;
的度數(shù)為 ;
②![]() ,
,![]() ,
,![]() 之間的關(guān)系是 .
之間的關(guān)系是 .

【答案】(1)見解析;(2)見解析;(3)①![]() ,②
,②![]() .
.
【解析】
(1)如圖1,先利用SAS證明![]() ,得到
,得到![]() ,進(jìn)一步可得證
,進(jìn)一步可得證![]() ;
;
(2)如圖2,過(guò)![]() 作
作![]() 交
交![]() 于
于![]() ,利用ASA證明
,利用ASA證明![]() ,得到
,得到![]() ,從而得證
,從而得證![]() ;
;
(3)①如圖3-1,在三角形內(nèi)作![]() ,
,![]() 交
交![]() 于
于![]() 點(diǎn),證得
點(diǎn),證得![]() 是等邊三角形,即可得證;
是等邊三角形,即可得證;
②先利用SAS證明![]() ,得到
,得到![]() ,再利用等量代換可證得結(jié)論.
,再利用等量代換可證得結(jié)論.
(1)如圖1,
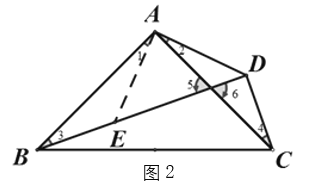
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,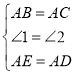
![]()
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ;
;
(2)如圖2,過(guò)![]() 作
作![]() 交
交![]() 于
于![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,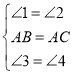 ,
,
![]()
![]() ,
,
![]() ,
,
![]() ;
;
(3)①如圖3-1,在三角形內(nèi)作![]() ,
,![]() 交
交![]() 于
于![]() 點(diǎn),
點(diǎn),
與(2)同理可證![]() ,
,
![]() 是等邊三角形,
是等邊三角形,
![]() ;
;
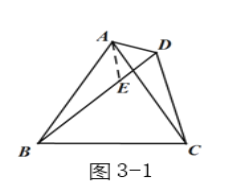
②![]() .
.
理由是:
如圖3-1,易知![]() ,
,
又AB=AC,由①知AE=AD,
![]()
![]() ,
,
![]() ,
,
![]() 是等邊三角形,
是等邊三角形,
![]()
![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案 目標(biāo)測(cè)試系列答案
目標(biāo)測(cè)試系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在矩形ABCD中,AB=8,BC=12,點(diǎn)E是BC的中點(diǎn),連接AE,將△ABE沿AE折疊,點(diǎn)B落在點(diǎn)F處,連接FC,則tan∠ECF=( )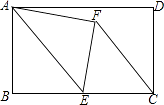
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
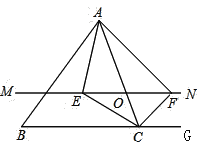
【題目】如圖,在![]() 中,點(diǎn)
中,點(diǎn)![]() 是
是![]() 邊上的一個(gè)動(dòng)點(diǎn),過(guò)點(diǎn)
邊上的一個(gè)動(dòng)點(diǎn),過(guò)點(diǎn)![]() 作直線
作直線![]() ,設(shè)
,設(shè)![]() 交
交![]() 的角平分線于點(diǎn)
的角平分線于點(diǎn)![]() ,交
,交![]() 的外角平分線于點(diǎn)
的外角平分線于點(diǎn)![]() .
.
(1)求證:![]() ;
;
(2)當(dāng)點(diǎn)![]() 運(yùn)動(dòng)到何處時(shí),四邊形
運(yùn)動(dòng)到何處時(shí),四邊形![]() 是矩形?并證明你的結(jié)論.
是矩形?并證明你的結(jié)論.
(3)當(dāng)點(diǎn)![]() 運(yùn)動(dòng)到何處,且
運(yùn)動(dòng)到何處,且![]() 滿足什么條件時(shí),四邊形
滿足什么條件時(shí),四邊形![]() 是正方形?并說(shuō)明理由.
是正方形?并說(shuō)明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】菱形ABCD中,∠B=60°,AB=4,點(diǎn)E在BC上,CE=2![]() ,若點(diǎn)P是菱形上異于點(diǎn)E的另一點(diǎn),CE=CP,則EP的長(zhǎng)為_____.
,若點(diǎn)P是菱形上異于點(diǎn)E的另一點(diǎn),CE=CP,則EP的長(zhǎng)為_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖所示,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D為AB邊上一點(diǎn).
(1)求證:△ACE≌△BCD;
(2)若AD=5,BD=12,求DE的長(zhǎng).

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】現(xiàn)有正方形ABCD和一個(gè)以O(shè)為直角頂點(diǎn)的三角板,移動(dòng)三角板,使三角板兩直角邊所在直線分別與直線BC,CD交于點(diǎn)M、N.
(1)如圖1,若點(diǎn)O與點(diǎn)A重合,則OM與ON的數(shù)量關(guān)系是;
(2)如圖2,若點(diǎn)O在正方形的中心(即兩對(duì)角線交點(diǎn)),則(1)中的結(jié)論是否仍然成立?請(qǐng)說(shuō)明理由;
(3)如圖3,若點(diǎn)O在正方形的內(nèi)部(含邊界),當(dāng)OM=ON時(shí),請(qǐng)?zhí)骄奎c(diǎn)O在移動(dòng)過(guò)程中可形成什么圖形?
(4)如圖4,是點(diǎn)O在正方形外部的一種情況.當(dāng)OM=ON時(shí),請(qǐng)你就“點(diǎn)O的位置在各種情況下(含外部)移動(dòng)所形成的圖形”提出一個(gè)正確的結(jié)論.(不必說(shuō)明)
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() 為
為![]() 上一點(diǎn),分別以
上一點(diǎn),分別以![]() ,
,![]() 為折痕將兩個(gè)角(
為折痕將兩個(gè)角(![]() ,
,![]() )向內(nèi)折起,點(diǎn)
)向內(nèi)折起,點(diǎn)![]() ,
,![]() 恰好都落在
恰好都落在![]() 邊的點(diǎn)
邊的點(diǎn)![]() 處.若
處.若![]() ,
,![]() ,則
,則![]() ________.
________.
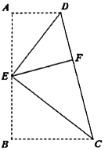
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在△ABC中,AD是BC邊上的中線,E是AD的中點(diǎn),過(guò)點(diǎn)A作BC的平行線與BE的延長(zhǎng)線相交于點(diǎn)F,連接CF.
(1)求證:四邊形CFAD為平行四邊形.
(2)若∠BAC=90°,AB=4,BD=![]() ,請(qǐng)求出四邊形CFAD的面積.
,請(qǐng)求出四邊形CFAD的面積.

查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com