
【題目】問題再現:
數形結合是解決數學問題的一種重要的思想方法,借助這種方法可將抽象的數學知識變得直觀起來并且具有可操作性,從而可以幫助我們快速解題.初中數學里的一些代數公式,很多都可以通過表示幾何圖形面積的方法進行直觀推導和解釋.
例如:利用圖形的幾何意義證明完全平方公式.
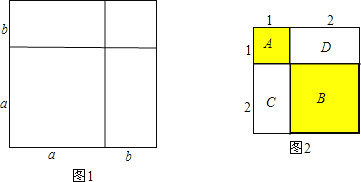
證明:將一個邊長為a的正方形的邊長增加b,形成兩個矩形和兩個正方形,如圖1:
這個圖形的面積可以表示成:
(a+b)2或 a2+2ab+b2
∴(a+b)2 =a2+2ab+b2
這就驗證了兩數和的完全平方公式.
類比解決:
(1)請你類比上述方法,利用圖形的幾何意義證明平方差公式.(要求畫出圖形并寫出推理過程)
問題提出:如何利用圖形幾何意義的方法證明:13+23=32?
如圖2,A表示1個1×1的正方形,即:1×1×1=13
B表示1個2×2的正方形,C與D恰好可以拼成1個2×2的正方形,因此:B、C、D就可以表示2個2×2的正方形,即:2×2×2=23而A、B、C、D恰好可以拼成一個(1+2)×(1+2)的大正方形.
由此可得:13+23=(1+2)2=32
嘗試解決:
(2)請你類比上述推導過程,利用圖形的幾何意義確定:13+23+33= .(要求寫出結論并構造圖形寫出推證過程).
(3)問題拓廣:
請用上面的表示幾何圖形面積的方法探究:13+23+33+…+n3= .(直接寫出結論即可,不必寫出解題過程)
【答案】(1)見解析;(2)62,推證過程見解析;(3)[![]() n(n+1)]2
n(n+1)]2
【解析】
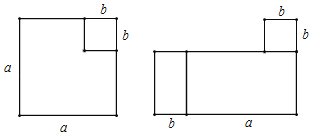
(1)類比解決:如圖:邊長為a,b的兩個正方形,邊保持平行,從大正方形中剪去小正方形,剩下的圖形可以分割成2個長方形并拼成一個大長方形.根據第一個圖形的陰影部分的面積是a2﹣b2,第二個圖形的陰影部分的面積是(a+b)(a﹣b),可以驗證平方差公式;
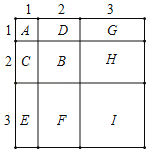
(2)嘗試解決:如圖,A表示一個1×1的正方形,B、C、D表示2個2×2的正方形,E、F、G表示3個3×3的正方形,而A、B、C、D、E、F、G恰好可以拼成一個邊長為(1+2+3)的大正方形,根據大正方形面積的兩種表示方法,可以得出13+23+33=62;
(3)問題拓廣:由上面表示幾何圖形的面積探究知,13+23+33+…+n3=(1+2+3+…+n)2,進一步化簡即可.
(1)∵如圖,左圖的陰影部分的面積是a2﹣b2,
右圖的陰影部分的面積是(a+b)(a﹣b),
∴a2﹣b2=(a+b)(a﹣b),
這就驗證了平方差公式;
(2)如圖,A表示1個1×1的正方形,即1×1×1=13;
B表示1個2×2的正方形,C與D恰好可以拼成1個2×2的正方形,
因此:B、C、D就可以表示2個2×2的正方形,即:2×2×2=23;
G與H,E與F和I可以表示3個3×3的正方形,即3×3×3=33;
而整個圖形恰好可以拼成一個(1+2+3)×(1+2+3)的大正方形,
由此可得:13+23+33=(1+2+3)2=62;
故答案為:62;
(3)由上面表示幾何圖形的面積探究可知,13+23+33+…+n3=(1+2+3+…+n)2,
又∵1+2+3+…+n=![]() n(n+1),
n(n+1),
∴13+23+33+…+n3=[![]() n(n+1)]2.
n(n+1)]2.
故答案為:[![]() n(n+1)]2.
n(n+1)]2.


 優生樂園系列答案
優生樂園系列答案科目:初中數學 來源: 題型:
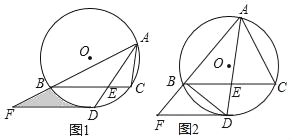
【題目】如圖1,△ABC內接于⊙O,∠BAC的平分線交⊙O于點D,交BC于點E(BE>EC),且BD=2![]() .過點D作DF∥BC,交AB的延長線于點F.
.過點D作DF∥BC,交AB的延長線于點F.
(1)求證:DF為⊙O的切線;
(2)若∠BAC=60°,DE=![]() ,求圖中陰影部分的面積;
,求圖中陰影部分的面積;
(3)若![]() ,DF+BF=8,如圖2,求BF的長.
,DF+BF=8,如圖2,求BF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
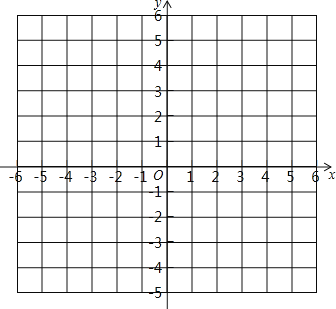
【題目】已知在平面直角坐標系中有三點![]() 、
、![]() 、
、![]() ,請回答如下問題:
,請回答如下問題:
(1)在坐標系內描出點![]() 的位置:
的位置:
(2)求出以![]() 三點為頂點的三角形的面積;
三點為頂點的三角形的面積;
(3)在![]() 軸上是否存在點
軸上是否存在點![]() ,使以
,使以![]() 三點為頂點的三角形的面積為10,若存在,請直接寫出點
三點為頂點的三角形的面積為10,若存在,請直接寫出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
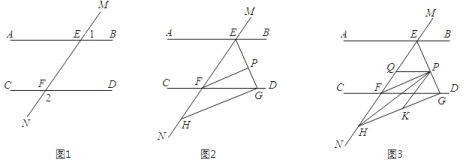
【題目】如圖 1,直線 MN 與直線 AB,CD 分別交于點 E,F,∠1 與∠2 互補.
(1)試判斷直線 AB 與直線 CD 的位置關系,并說明理由;
(2)如圖 2,∠BEF 與∠EFD 的角平分線交于點 P,EP 與 CD 交于點 G,點 H 是 MN 上一點,且GH⊥EG,求證:PF∥GH;
(3)如圖 3,在(2)的條件下,連結 PH,在 GH 上取一點 K,使得∠PKG=2∠HPK,過點 P 作 PQ 平分∠EPK 交 EF 于點 Q,問∠HPQ 的大小是否發生變化?若不變,請求出其值;若變化,說明理由.(溫馨提示:三角形的三個內角和為 180°)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在Rt△ABC中,∠C=90°,AC=6,BC=8,動點P從點A開始沿邊AC向點C以1個單位長度的速度運動,動點Q從點C開始沿邊CB向點B以每秒2個單位長度的速度運動,過點P作PD∥BC,交AB于點D,連接PQ分別從點A、C同時出發,當其中一點到達端點時,另一點也隨之停止運動,設運動時間為t秒(t≥0).
(1)直接用含t的代數式分別表示:QB= ,PD= .
(2)是否存在t的值,使四邊形PDBQ為菱形?若存在,求出t的值;若不存在,說明理由.并探究如何改變Q的速度(勻速運動),使四邊形PDBQ在某一時刻為菱形,求點Q的速度;
(3)如圖2,在整個運動過程中,求出線段PQ中點M所經過的路徑長.

查看答案和解析>>
科目:初中數學 來源: 題型:
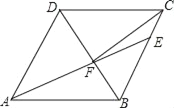
【題目】如圖,在菱形ABCD中,AB=6,∠DAB=60°,AE分別交BC、BD于點E、F,CE=2,連接CF,以下結論:①△ABF≌△CBF;②點E到AB的距離是2![]() ;③tan∠DCF=
;③tan∠DCF=![]() ;④△ABF的面積為
;④△ABF的面積為![]() .其中一定成立的有幾個( )
.其中一定成立的有幾個( )
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:△ABC是三邊都不相等的三角形,點O和點P是這個三角形內部兩點.
(1)如圖①,如果點P是這個三角形三個內角平分線的交點,那么∠BPC和∠BAC有怎樣的數量關系?請說明理由;
(2)如圖②,如果點O是這個三角形三邊垂直平分線的交點,那么∠BOC和∠BAC有怎樣的數量關系?請說明理由;
(3)如圖③,如果點P(三角形三個內角平分線的交點),點O(三角形三邊垂直平分線的交點)同時在不等邊△ABC的內部,那么∠BPC和∠BOC有怎樣的數量關系?請直接回答.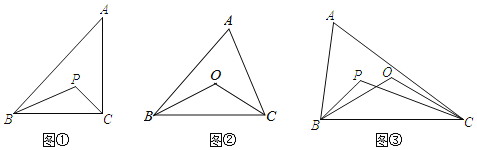
查看答案和解析>>
科目:初中數學 來源: 題型:
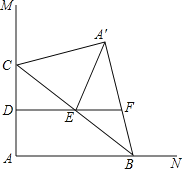
【題目】如圖,∠MAN=90°,點C在邊AM上,AC=4,點B為邊AN上一動點,連接BC,△A′BC與△ABC關于BC所在直線對稱,點D,E分別為AC,BC的中點,連接DE并延長交A′B所在直線于點F,連接A′E.當△A′EF為直角三角形時,AB的長為_____.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com