
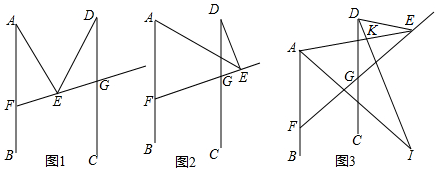
分析 (1)過E作EH∥AB,根據兩直線平行,內錯角相等,即可得出∠AED=∠AEH+∠DEH=∠EAF+∠EDG;
(2)設CD與AE交于點H,根據∠EHG是△DEH的外角,即可得出∠EHG=∠AED+∠EDG,進而得到∠EAF=∠AED+∠EDG;
(3)設∠EAI=∠BAI=α,則∠CHE=∠BAE=2α,進而得出∠EDI=α+10°,∠CDI=$\frac{1}{2}$α+5°,再根據∠CHE是△DEH的外角,可得∠CHE=∠EDH+∠DEK,即2α=$\frac{1}{2}$α+5°+α+10°+20°,求得α=70°,即可根據三角形內角和定理,得到∠EKD的度數.
解答 解:(1)∠AED=∠EAF+∠EDG.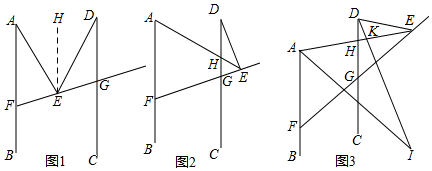
理由:如圖1,過E作EH∥AB,
∵AB∥CD,
∴AB∥CD∥EH,
∴∠EAF=∠AEH,∠EDG=∠DEH,
∴∠AED=∠AEH+∠DEH=∠EAF+∠EDG;
(2)證明:如圖2,設CD與AE交于點H,
∵AB∥CD,
∴∠EAF=∠EHG,
∵∠EHG是△DEH的外角,
∴∠EHG=∠AED+∠EDG,
∴∠EAF=∠AED+∠EDG;
(3)∵AI平分∠BAE,
∴可設∠EAI=∠BAI=α,則∠BAE=2α,
∵AB∥CD,
∴∠CHE=∠BAE=2α,
∵∠AED=20°,∠I=30°,∠DKE=∠AKI,
∴∠EDI=α+30°-20°=α+10°,
又∵∠EDI:∠CDI=2:1,
∴∠CDI=$\frac{1}{2}$∠EDK=$\frac{1}{2}$α+5°,
∵∠CHE是△DEH的外角,
∴∠CHE=∠EDH+∠DEK,
即2α=$\frac{1}{2}$α+5°+α+10°+20°,
解得α=70°,
∴∠EDK=70°+10°=80°,
∴△DEK中,∠EKD=180°-80°-20°=80°.
點評 本題主要考查了平行線的性質,三角形外角性質以及三角形內角和定理的綜合應用,解決問題的關鍵是作輔助線構造內錯角,運用三角形外角性質進行計算求解.解題時注意:三角形的一個外角等于和它不相鄰的兩個內角的和.


科目:初中數學 來源: 題型:解答題
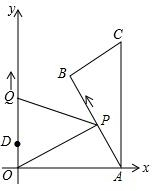 如圖,Rt△ABC中,∠B=90°,∠CAB=30°,AC⊥x軸,它的頂點A的坐標為(10,0),C(10,$\frac{20\sqrt{3}}{3}$),點P從點A出發,沿A→B→C的方向勻速運動,同時點Q從點D(0,2)出發,沿y軸正方向以相同速度運動,當點P到達點C時,兩點同時停止運動,若P點的速度為2單位/秒,設P運動的時間為t秒.
如圖,Rt△ABC中,∠B=90°,∠CAB=30°,AC⊥x軸,它的頂點A的坐標為(10,0),C(10,$\frac{20\sqrt{3}}{3}$),點P從點A出發,沿A→B→C的方向勻速運動,同時點Q從點D(0,2)出發,沿y軸正方向以相同速度運動,當點P到達點C時,兩點同時停止運動,若P點的速度為2單位/秒,設P運動的時間為t秒.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
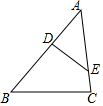 如圖,在△ABC的邊AB、AC上有點D、E.若∠BDE+∠C=180°,求證:$\frac{AD}{AC}$=$\frac{AE}{AB}$.
如圖,在△ABC的邊AB、AC上有點D、E.若∠BDE+∠C=180°,求證:$\frac{AD}{AC}$=$\frac{AE}{AB}$.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 向東走20千米與向西走15千米 | B. | 收入200元與虧損30元 | ||
| C. | 超過0.05mm與不足0.03mm | D. | 上升10米和下降7米 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
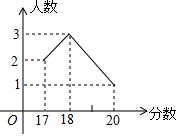 某校6名學生的某次競賽成績統計如圖,則這組數據的眾數、中位數、方差依次是( )
某校6名學生的某次競賽成績統計如圖,則這組數據的眾數、中位數、方差依次是( )| A. | 18,17.5,5 | B. | 18,17.5,3 | C. | 18,18,3 | D. | 18,18,1 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
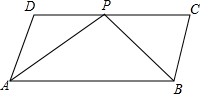 如圖,ABCD是平行四邊形,P是CD上一點,且AP和BP分別平分∠DAB和∠CBA.
如圖,ABCD是平行四邊形,P是CD上一點,且AP和BP分別平分∠DAB和∠CBA.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com