
 如圖,點P是菱形ABCD的對角線DB延長線上一點,連接PC并延長,交AD延長線于點E,AB延長線于點F.
如圖,點P是菱形ABCD的對角線DB延長線上一點,連接PC并延長,交AD延長線于點E,AB延長線于點F.分析 (1)先由菱形的性質得出BC=BA,∠CBD=∠ABD,進而判斷出△PAB≌△PCB;
(2)借助(1)的結論得出∠PAB=∠PCB,再用菱形的性質得出∠PAB=∠E,進而判斷出結論;
(3)借助(2)的相似得出比例式求出PE,即可求出EF.
解答 解(1)∵四邊形ABCD是菱形,
∴BC=BA,∠CBD=∠ABD,
∴∠CBP=∠ABP,
在△PAB和△PCB中,$\left\{\begin{array}{l}{BC=BA}\\{∠CBP=∠ABP}\\{BP=BP}\end{array}\right.$,
∴△PAB≌△PCB,
(2)由(1)知,△PAB≌△PCB,
∴∠PAB=∠PCB,
∵四邊形ABCD是菱形,
∴BC∥AE,
∴∠PCB=∠E,
∴∠PAB=∠E,
∵∠APF=∠EPA,
∴△PAF∽△PEA,
(3)由(2)知,△PAF∽△PEA,
∴$\frac{PA}{PE}=\frac{PF}{PA}$,
∴$\frac{6}{PE}=\frac{2}{6}$,
∴PE=18,
∴EF=PE-FP=16.
點評 此題是相似形綜合題,主要考查了菱形的性質,全等三角形的判定和性質,相似三角形的判定和性質,判斷出△PAB≌△PCB是解本題的關鍵,是一道中等難度的中考常考題.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:選擇題
| A. | ±$\sqrt{25}$=5 | B. | -$\sqrt{{5}^{2}}$=±5 | C. | $\sqrt{(-2)^{2}}$=2 | D. | $\sqrt{4\frac{1}{4}}$=2$\frac{1}{2}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

| 圖① | 圖② | 圖③ | |
| 三個角上三個數的積 | 1×(-1)×2=-2 | (-3)×(-4)×(-5)=-60 | ② |
| 三個角上三個數的和 | 1+(-1)+2=2 | (-3)+(-4)+(-5)=-12 | ③ |
| 積與和的商 | (-2)÷2=-1 | ① | ④ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
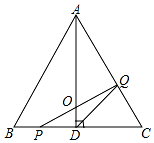 如圖,在△ABC中,已知AB=BC=CA=4cm,AD⊥BC于D,點P、Q分別從B、C兩點同時出發,其中點P沿BC向終點C運動,速度為1cm/s;點Q沿CA向終點A運動,速度為2cm/s,當一個到達終點時,另一個也停止運動.設它們運動的時間為x(s).
如圖,在△ABC中,已知AB=BC=CA=4cm,AD⊥BC于D,點P、Q分別從B、C兩點同時出發,其中點P沿BC向終點C運動,速度為1cm/s;點Q沿CA向終點A運動,速度為2cm/s,當一個到達終點時,另一個也停止運動.設它們運動的時間為x(s).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com