
(1)觀察發現
如題(a)圖,若點A,B在直線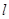 同側,在直線
同側,在直線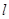 上找一點P,使AP+BP的值最小.
上找一點P,使AP+BP的值最小.
做法如下:作點B關于直線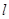 的對稱點
的對稱點 ,連接
,連接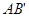 ,與直線
,與直線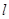 的交點就是所求的點P
的交點就是所求的點P
再如題(b)圖,在等邊三角形ABC中,AB=2,點E是AB的中點,AD是高,在AD上找一點P,使BP+PE的值最小.
做法如下:作點B關于AD的對稱點,恰好與點C重合,連接CE交AD于一點,則這點就是所求的點P,故BP+PE的最小值為 .

(2)實踐運用
如題(c)圖,已知⊙O的直徑CD為4,AD的度數為60°,點B是弧AD的中點,在直徑CD上找一點P,使BP+AP的值最小,并求BP+AP的最小值.

(3)拓展延伸
如題(d)圖,在四邊形ABCD的對角線AC上找一點P,使∠APB=∠APD.保留作圖痕跡,不必寫出作法.
(1)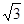 ;(2)
;(2)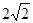 ;(3)如圖所示:
;(3)如圖所示:
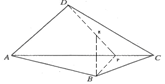
【解析】
試題分析:(1)根據等邊三角形的性質及勾股定理求解即可;
(2)作點B關于CD的對稱點E,則點E正好在圓周上,連接OA、OB、OE,連接AE交CD與一點P,AP+BP最短,先根據軸對稱性證得△OBE為等邊三角形,即可證得△OAE為等腰直角三角形,從而求得結果;
(3)找B關于AC對稱點E,連DE延長交AC于P即可.
(1)BP+PE的最小值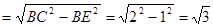 ;
;
(2)作點B關于CD的對稱點E,則點E正好在圓周上,連接OA、OB、OE,連接AE交CD與一點P,AP+BP最短,
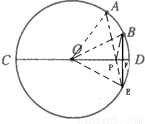
因為AD的度數為60°,點B是弧AD的中點,
所以∠AEB=15°,
因為B關于CD的對稱點E,
所以∠BOE=60°,
所以△OBE為等邊三角形,
所以∠OEB=60°,
所以∠OEA=45°,
又因為OA=OE,
所以△OAE為等腰直角三角形,
所以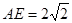 ;
;
(3)找B關于AC對稱點E,連DE延長交AC于P即可,如圖所示:
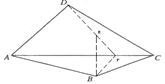
考點:軸對稱-最短路線問題
點評:解決此類問題,一般都是運用軸對稱的性質,將求折線問題轉化為求線段問題,其說明最短的依據是三角形兩邊之和大于第三邊.


科目:初中數學 來源: 題型:
1.觀察發現
如題27(a)圖,若點A,B在直線![]() 同側,在直線
同側,在直線![]() 上找一點P,使AP+BP的值最小. 做法如下:作點B關于直線
上找一點P,使AP+BP的值最小. 做法如下:作點B關于直線![]() 的對稱點
的對稱點![]() ,連接
,連接![]() ,與直線
,與直線![]() 的交點就是所求的點P
的交點就是所求的點P
再如題27(b)圖,在等邊三角形ABC中,AB=2,點E是AB的中點,AD是高,在AD上找一點P,使BP+PE的值最小.
如下:作點B關于AD的對稱點,恰好與點C重合,連接CE交AD于一點,則這
點就是所求的點P,故BP+PE的最小值為 .

2.實踐運用
如題27(c)圖,已知⊙O的直徑CD為4,弧AD所對圓心角的度數為60°,點B是弧AD的中點,請你在直徑CD上找一點P,使BP+AP的值最小,并求BP+AP的最小值.

3.拓展延伸
如題27(d)圖,在四邊形ABCD的對角線AC上找一點P,使∠APB=∠APD.保留
作圖痕跡,不必寫出作法.

查看答案和解析>>
科目:初中數學 來源: 題型:
觀察發現
如題26(a)圖,若點A,B在直線同側,在直線
上找一點P,使AP+BP的值最小.
做法如下:作點B關于直線的對稱點
,連接
,與直線
的交點就是所求的點P
再如題26(b)圖,在等邊三角形ABC中,AB=2,點E是AB的中點,AD是高,在AD上找一點P,使BP+PE的值最小.
做法如下:作點B關于AD的對稱點,恰好與點C重合,連接CE交AD于一點,則這
點就是所求的點P,故BP+PE的最小值為 .
題26(a)圖 題26(b)圖
(2)實踐運用
如題26(c)圖,已知⊙O的直徑CD為4,AD的度數為60°,點B是的中點,在直徑CD上找一點P,使BP+AP的值最小,并求BP+AP的最小值.
題26(c)圖 題26(d)圖
(3)拓展延伸
如題26(d)圖,在四邊形ABCD的對角線AC上找一點P,使∠APB=∠APD.保留
作圖痕跡,不必寫出作法.
查看答案和解析>>
科目:初中數學 來源: 題型:
 同側,在直線
同側,在直線 上找一點P,使AP+BP的值最小.
上找一點P,使AP+BP的值最小. 的對稱點
的對稱點 ,連接
,連接 ,與直線
,與直線 的交點就是所求的點P
的交點就是所求的點P
 的中點,在直徑CD上找一點P,使BP+AP的值最小,并求BP+AP的最小值.
的中點,在直徑CD上找一點P,使BP+AP的值最小,并求BP+AP的最小值.

查看答案和解析>>
科目:初中數學 來源:2012屆江西省南昌市九年級下學期4月考數學卷(帶解析) 題型:解答題
(1)觀察發現如題(a)圖,若點A,B在直線 同側,在直線
同側,在直線 上找一點P,使AP+BP的值最小. 做法如下:作點B關于直線
上找一點P,使AP+BP的值最小. 做法如下:作點B關于直線 的對稱點
的對稱點 ,連接
,連接 ,與直線
,與直線 的交點就是所求的點P 再如題(b)圖,在等邊三角形ABC中,AB=2,點E是AB的中點,AD是高,在AD上找一點P,使BP+PE的值最小. 做法如下:作點B關于AD的對稱點,恰好與點C重合,連接CE交AD于一點,則這點就是所求的點P,故BP+PE的最小值為 .
的交點就是所求的點P 再如題(b)圖,在等邊三角形ABC中,AB=2,點E是AB的中點,AD是高,在AD上找一點P,使BP+PE的值最小. 做法如下:作點B關于AD的對稱點,恰好與點C重合,連接CE交AD于一點,則這點就是所求的點P,故BP+PE的最小值為 . 
(2)實踐運用
如題(c)圖,已知⊙O的直徑CD為4,弧AD所對圓心角的度數為60°,點B是弧AD的中點,請你在直徑CD上找一點P,使BP+AP的值最小,并求BP+AP的最小值.
(3)拓展延伸
如題(d)圖,在四邊形ABCD的對角線AC上找一點P,使∠APB=∠APD.保留
作圖痕跡,不必寫出作法.
查看答案和解析>>
科目:初中數學 來源:2011-2012學年江西省南昌市九年級下學期第二次聯考數學試卷(解析版) 題型:解答題
1.觀察發現
如題27(a)圖,若點A,B在直線 同側,在直線
同側,在直線 上找一點P,使AP+BP的值最小. 做法如下:作點B關于直線
上找一點P,使AP+BP的值最小. 做法如下:作點B關于直線 的對稱點
的對稱點 ,連接
,連接 ,與直線
,與直線 的交點就是所求的點P
的交點就是所求的點P
再如題27(b)圖,在等邊三角形ABC中,AB=2,點E是AB的中點,AD是高,在AD上找一點P,使BP+PE的值最小.
如下:作點B關于AD的對稱點,恰好與點C重合,連接CE交AD于一點,則這
點就是所求的點P,故BP+PE的最小值為 .

2.實踐運用
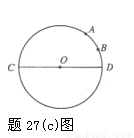
如題27(c)圖,已知⊙O的直徑CD為4,弧AD所對圓心角的度數為60°,點B是弧AD的中點,請你在直徑CD上找一點P,使BP+AP的值最小,并求BP+AP的最小值.
3.拓展延伸
如題27(d)圖,在四邊形ABCD的對角線AC上找一點P,使∠APB=∠APD.保留
作圖痕跡,不必寫出作法.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com