
 -
- -
-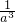 ,則a+
,則a+ =________
=________ +
+ +
+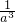 =0,然后分組,分別利用立方和公式、完全平方公式、分解因式得到(a+
=0,然后分組,分別利用立方和公式、完全平方公式、分解因式得到(a+ )(a+
)(a+ +3)(a+
+3)(a+ -2)=0,由此即可求出結果.
-2)=0,由此即可求出結果. -
- -
-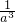 ,
, +
+ +
+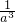 =0,
=0,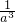 +a2+
+a2+ +2-3(a+
+2-3(a+ )=0,
)=0, )(a2-1+
)(a2-1+ )+(a+
)+(a+ )2-3(a+
)2-3(a+ )=0,
)=0, )(a2-1+
)(a2-1+ +a+
+a+ -3)=0,
-3)=0, )[(a+
)[(a+ )2+(a+
)2+(a+ )-6]=0,
)-6]=0, )(a+
)(a+ +3)(a+
+3)(a+ -2)=0,
-2)=0, ≠0,
≠0, +3=0,或a+
+3=0,或a+ -2=0,
-2=0, =-3或2.
=-3或2.

 天天向上口算本系列答案
天天向上口算本系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com