
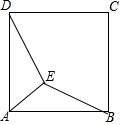
 如圖,點E是正方形ABCD內一點,DE=2,AE=1,EB=$\sqrt{2}$
如圖,點E是正方形ABCD內一點,DE=2,AE=1,EB=$\sqrt{2}$分析 (1)根據旋轉中心、旋轉方向和旋轉角度,畫出△AED繞點A順時針旋轉90度后的圖形;
(2)根據旋轉的性質,可得△AEF是等腰直角三角形,根據勾股定理的逆定理,可得△BEF是等腰直角三角形,且∠BEF=90°,進而得到∠AEB=∠AEF+∠BEF=135°;
(3)根據△AEF和△BEF都是等腰直角三角形,可得∠AFB=90°,再根據Rt△ABF中,AB2=AF2+BF2=1+4=5,可得正方形ABCD的面積.
解答 解:(1)如圖所示,△ABF即為所求;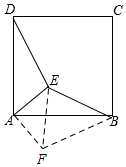
(2)∵△ADE繞點A順時針旋轉90度后得到△ABF,
∴AE=AF=1,∠EAF=90°,DE=BF=2,
∴△AEF是等腰直角三角形,
∴∠AEF=45°,EF=$\sqrt{2}$,
又∵EB=$\sqrt{2}$,
∴BE2+EF2=4=BF2,
∴△BEF是等腰直角三角形,且∠BEF=90°,
∴∠AEB=∠AEF+∠BEF=45°+90°=135°;
(3)由(2)可得,△AEF和△BEF都是等腰直角三角形,
∴∠AFE=∠BFE=45°,
∴∠AFB=90°,
∴Rt△ABF中,AB2=AF2+BF2=1+4=5,
∴正方形ABCD的面積=AB2=5.
點評 本題主要考查了旋轉的性質,正方形的性質,勾股定理及其逆定理的綜合應用,解決問題的關鍵是掌握旋轉的性質:旋轉前、后的圖形全等.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 若|a|=-a,則a<0 | B. | 若a<0,ab<0,則b>0 | ||
| C. | 若ab>0,則a>0,b>0 | D. | 若a=b,m是有理數,則$\frac{a}{m}$=$\frac{b}{m}$ |
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com