
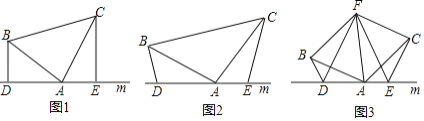
【題目】如圖(1),已知:在![]() 中,
中,![]() ,
,![]() ,直線
,直線![]() 經過點
經過點![]() ,
,![]() 直線
直線![]() ,
,![]() 直線
直線![]() ,垂足分別為點
,垂足分別為點![]() 、
、![]() .證明:
.證明:![]() .
.
(2)如圖(2),將(1)中的條件改為:在![]() 中,
中,![]() ,
,![]() 、
、![]() 、
、![]() 三點都在直線
三點都在直線![]() 上,并且有
上,并且有![]() .請直接寫出線段
.請直接寫出線段![]() 、
、![]() 和
和![]() 之間的數量關系.
之間的數量關系.
(3)拓展與應用:如圖(3),![]() 、
、![]() 是
是![]() 、
、![]() 、
、![]() 三點所在直線
三點所在直線![]() 上的兩動點
上的兩動點![]() 、
、![]() 、
、![]() 三點互不重合),點
三點互不重合),點![]() 為
為![]() 平分線上的一點,且
平分線上的一點,且![]() 和
和![]() 均為等邊三角形,連接
均為等邊三角形,連接![]() 、
、![]() ,若
,若![]() ,試證明
,試證明![]() .
.
 初中學業考試導與練系列答案
初中學業考試導與練系列答案科目:初中數學 來源: 題型:
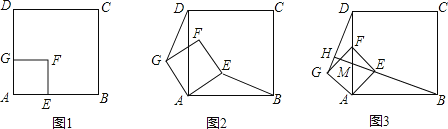
【題目】如圖1,四邊形ABCD,AEFG都是正方形,E、G分別在AB、AD邊上,已知AB=4.
(1)求正方形ABCD的周長;
(2)將正方形AEFG繞點A逆時針旋轉θ(0°<θ<90°)時,如圖2,求證:BE=DG.
(3)將正方形AEFG繞點A逆時針旋轉45°時,如圖3,延長BE交DG于點H,設BH與AD的交點為M.
①求證:BH⊥DG;
②當AE=![]() 時,求線段BH的長(精確到0.1).
時,求線段BH的長(精確到0.1).
查看答案和解析>>
科目:初中數學 來源: 題型:
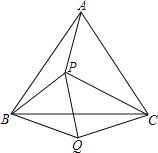
【題目】如圖,P是等邊三角形ABC內的一點,且PA=3,PB=4,PC=5,以BC為邊在△ABC外作△BQC≌△BPA,連接PQ,則以下結論中正確有_____(填序號)①△BPQ是等邊三角形②△PCQ是直角三角形③∠APB=150° ④∠APC=120°
查看答案和解析>>
科目:初中數學 來源: 題型:
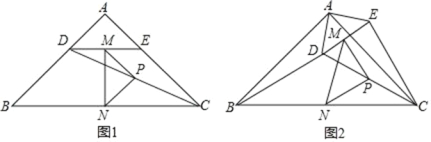
【題目】如圖 1,在 Rt△ABC 中,∠A=90°,AB=AC,點 D、E 分別在邊 AB、AC 上,AD=AE,連接DC,點 M、P、N 分別為 DE、DC、BC 的中點,
(1)觀察猜想:如圖 1 中,△PMN 是 三角形;
(2)探究證明:把△ADE 繞點 A 逆時針方向旋轉到圖 2 的位置,連接 MN,BD, CE.判斷△PMN 的形狀,并說明理由;
(3)拓展延伸:將△ADE 繞點 A 在平面內自由旋轉,若 AD=4,AB=10,請求△PMN 面積的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線y=x2+bx+c經過A(﹣1,0)、B(3,0)兩點.
(1)請求出拋物線的解析式;
(2)當0<x<4時,請直接寫出y的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
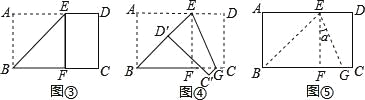
【題目】將長方形紙片 ABCD 沿過點 B 的直線折疊,使點 A 落在 BC 邊上的點 F 處, 折痕為 BE(如圖③);再沿過點 E 的直線折疊,使點 D 落在 BE 上的點處 D′,折痕為 EG(如圖④);再展平紙片(如圖⑤),則圖⑤中∠α=________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某鄉鎮風力資源豐富,為了實現低碳環保,該鄉鎮決定開展風力發電,打算購買10臺風力發電機組.現有A,B兩種型號機組,其中A型機組價格為12萬元/臺,月均發電量為2.4萬kw.h;B型機組價格為10萬元/臺,月均發電量為2萬kw.h.經預算該鄉鎮用于購買風力發電機組的資金不高于105萬元.
(1)請你為該鄉鎮設計幾種購買方案;
(2)如果該鄉鎮用電量不低于20.4萬kw.h/月,為了節省資金,應選擇那種購買方案?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx+c的圖象如圖所示,下列結論:①9a﹣3b+c=0;②4a﹣2b+c>0;③方程ax2+bx+c﹣4=0有兩個相等的實數根;④方程a(x﹣1)2+b(x﹣1)+c=0的兩根是x1=﹣2,x2=2.其中正確結論的個數是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,在![]() 中,
中,![]() ,
,![]() ,以A為圓心,任意長為半徑畫弧分別交AB、AC于點M和N再分別以MN為圓心,大于
,以A為圓心,任意長為半徑畫弧分別交AB、AC于點M和N再分別以MN為圓心,大于![]() 的長為半徑畫弧,兩弧交于點P,連接AP并延長交BC于點D,則下列說法中正確的有________.
的長為半徑畫弧,兩弧交于點P,連接AP并延長交BC于點D,則下列說法中正確的有________.
①AD是![]() 的平分線;②
的平分線;②![]() ;③點D在AB的中垂線上;④
;③點D在AB的中垂線上;④![]()

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com