
分析 根據題意畫出圖形,先求出∠AOB的度數,證明△AOB是等邊三角形,得出AB=OA,再根據直角三角形的性質求出OA的長,再根據S六邊形=6S△AOB即可得出結論.
解答 解:∵圖中是正六邊形,
∴∠AOB═60°.
∵OA=OB,
∴△OAB是等邊三角形.
∴OA=OAB=AB,
∵OD⊥AB,OD=$\sqrt{3}$,
∴OA=$\frac{OD}{sin60°}$=2.
∴AB=4,
∴S△AOB=$\frac{1}{2}$AB×OD=$\frac{1}{2}$×2×$\sqrt{3}$=$\sqrt{3}$,
∴正六邊形的面積=6S△AOB=6×$\sqrt{3}$=6$\sqrt{3}$.
故答案為:6$\sqrt{3}$.
點評 本題考查的是正多邊形和圓,熟知正六邊形的性質,求出△AOB的面積是解答此題的關鍵.


 黃岡創優卷系列答案
黃岡創優卷系列答案科目:初中數學 來源: 題型:選擇題
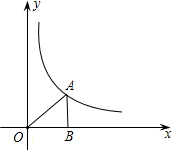 如圖,A為反比例函數y=$\frac{k}{x}$的圖象上一點,AB垂直x軸于B,若S△AOB=2,則k的值為( )
如圖,A為反比例函數y=$\frac{k}{x}$的圖象上一點,AB垂直x軸于B,若S△AOB=2,則k的值為( )| A. | 4 | B. | 2 | C. | -2 | D. | 1 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 有理數在數軸上的對應點的位置如圖所示,則下列結論正確的是( )
有理數在數軸上的對應點的位置如圖所示,則下列結論正確的是( )| A. | ab>0 | B. | a-b>0 | C. | $\frac{a}{b}>0$ | D. | b-a>0 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com