
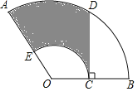
【題目】如圖,扇形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中點,
的中點,![]() ⊥
⊥![]() 交
交![]() 于點
于點![]() ,以
,以![]() 為半徑的
為半徑的![]() 交
交![]() 于點
于點![]() ,則圖中陰影部分的面積是___.
,則圖中陰影部分的面積是___.
科目:初中數學 來源: 題型:
【題目】一個盒子里裝有兩個紅球,兩個白球和一個藍球,這些球除顏色外都相同.從中隨機摸出一個球,記下顏色后放回,再從中隨機摸出一個球,兩次摸到的球的顏色能配成紫色(紅色和藍色能配成紫色)的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】央視舉辦的《中國詩詞大會》受到廣大學生群體廣泛關注.某校的詩歌朗誦社團就《中國詩詞大會》節目的喜愛程度,在校內對部分學生進行了問卷調查,并對問卷調查的結果分為“非常喜歡”、“比較喜歡”、“感覺一般”、“不太喜歡”四個等級,分別記作A、B、C、D.根據調查結果繪制出如圖所示的扇形統計圖和條形統計圖,請結合圖中說給信息解答下列問題:
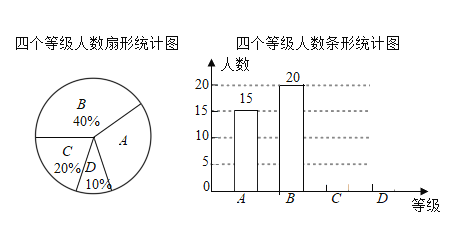
(1)本次被調查對象共有 人,扇形統計圖中被調查者“非常喜歡”等級所對應圓心角的度數為 ;
(2)將條形統計圖補充完整,并標明數據;
(3)若選“不太喜歡”的人中有兩名女生,其余是男生,從原“不太喜歡”的人中挑選兩名學生了解不太喜歡的原因,請用畫樹狀圖或列表法求所選取的這兩名學生恰好是一男一女的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】攀枝花得天獨厚,氣候宜人,農產品資源極為豐富,其中晚熟芒果遠銷北上廣等大城市.某水果店購進一批優質晚熟芒果,進價為10元/千克,售價不低于15元/千克,且不超過40元/每千克,根據銷售情況,發現該芒果在一天內的銷售量![]() (千克)與該天的售價
(千克)與該天的售價![]() (元/千克)之間的數量滿足如下表所示的一次函數關系.
(元/千克)之間的數量滿足如下表所示的一次函數關系.
銷售量 | … | 32.5 | 35 | 35.5 | 38 | … |
售價 | … | 27.5 | 25 | 24.5 | 22 | … |
(1)某天這種芒果售價為28元/千克.求當天該芒果的銷售量
(2)設某天銷售這種芒果獲利![]() 元,寫出
元,寫出![]() 與售價
與售價![]() 之間的函數關系式.如果水果店該天獲利400元,那么這天芒果的售價為多少元?
之間的函數關系式.如果水果店該天獲利400元,那么這天芒果的售價為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某書店以![]() 元的價格購進一批科普書進行銷售,物價局根據市場行情規定,銷售單價不低于
元的價格購進一批科普書進行銷售,物價局根據市場行情規定,銷售單價不低于![]() 元且不高于
元且不高于![]() 元.在銷售中發現,該科普書的每天銷售數量
元.在銷售中發現,該科普書的每天銷售數量![]() (本)與銷售單價
(本)與銷售單價![]() (元)之間存在某種函數關系,對應如下:
(元)之間存在某種函數關系,對應如下:
銷售單價 |
|
|
|
|
|
銷售數量 |
|
|
|
|
|
(1)用你所學過的函數知識,求出![]() 與
與![]() 之間的函數關系式;
之間的函數關系式;
(2)請問該科普書每天利潤![]() (元)的最大值是多少?
(元)的最大值是多少?
(3)如果該科普書每天利潤必須不少于![]() 元,試求出每天銷售數量
元,試求出每天銷售數量![]() 最少為多少本?
最少為多少本?
查看答案和解析>>
科目:初中數學 來源: 題型:
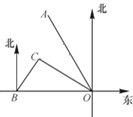
【題目】如圖所示,港口B位于港口O正西方向120 km處,小島C位于港口O北偏西60°的方向.一艘游船從港口O出發,沿OA方向(北偏西30°)以v km/h的速度駛離港口O,同時一艘快艇從港口B出發,沿北偏東30°的方向以60 km/h的速度駛向小島C,在小島C用1 h加裝補給物資后,立即按原來的速度給游船送去.
(1)快艇從港口B到小島C需要多長時間?
(2)若快艇從小島C到與游船相遇恰好用時1h,求v的值及相遇處與港口O的距離.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,菱形ABCD的邊長為20cm,∠ABC=120°.動點P、Q同時從點A出發,其中P以4cm/s的速度,沿A→B→C的路線向點C運動;Q先以2![]() cm/s的速度沿A→O的路線向點O運動,然后再以2cm/s的速度沿O→D的路線向點D運動,當P、Q到達終點時,整個運動隨之結束,設運動時間為t秒.
cm/s的速度沿A→O的路線向點O運動,然后再以2cm/s的速度沿O→D的路線向點D運動,當P、Q到達終點時,整個運動隨之結束,設運動時間為t秒.
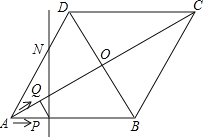
(1)在點P在AB上運動時,判斷PQ與對角線AC的位置關系,并說明理由;
(2)若點Q關于菱形ABCD的對角線交點O的對稱點為M,過點P且垂直于AB的直線l交菱形ABCD的邊AD(或CD)于點N.
①直接寫出當△PQM是直角三角形時t的取值范圍;
②是否存在這樣的t,使△PMN是以PN為一直角邊的直角三角形?若存在,請求出所有符合條件的t的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某養豬場對豬舍進行噴藥消毒.在消毒的過程中,先經過![]() 的藥物集中噴灑,再封閉豬舍
的藥物集中噴灑,再封閉豬舍![]() ,然后再打開窗戶進行通風.已知室內每立方米空氣中含藥量
,然后再打開窗戶進行通風.已知室內每立方米空氣中含藥量![]() (
(![]() )與藥物在空氣中的持續時間
)與藥物在空氣中的持續時間![]() (
(![]() )之間的函數圖象如圖所示,其中在打開窗戶通風前
)之間的函數圖象如圖所示,其中在打開窗戶通風前![]() 與
與![]() 分別滿足兩個一次函數,在通風后
分別滿足兩個一次函數,在通風后![]() 與
與![]() 滿足反比例函數.
滿足反比例函數.
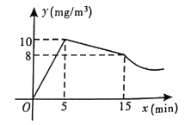
(1)求反比例函數的關系式;
(2)當豬舍內空氣中含藥量不低于![]() 且持續時間不少于
且持續時間不少于![]() ,才能有效殺死病毒,問此次消毒是否有效?
,才能有效殺死病毒,問此次消毒是否有效?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,拋物線y=ax2+bx+c的頂點坐標為(2,9),與y軸交于點A(0,5),與x軸交于點E、B.
(1)求二次函數y=ax2+bx+c的表達式;
(2)過點A作AC平行于x軸,交拋物線于點C,點P為拋物線上的一點(點P在AC上方),作PD平行于y軸交AB于點D,問當點P在何位置時,四邊形APCD的面積最大?并求出最大面積;
(3)若點M在拋物線上,點N在其對稱軸上,使得以A、E、N、M為頂點的四邊形是平行四邊形,且AE為其一邊,求點M、N的坐標.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com