
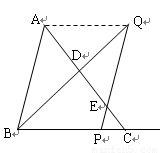
如圖,已知△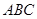 中,
中,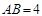 ,
,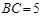 ,
,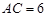 ,把線段
,把線段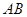 沿射線
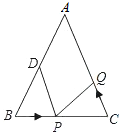
沿射線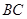 方向平移至PQ,直線PQ與直線AC交于點E,又聯結BQ與直線AC交于點D.
方向平移至PQ,直線PQ與直線AC交于點E,又聯結BQ與直線AC交于點D.
(1)若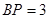 ,求
,求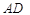 的長;
的長;
(2)設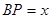 ,
,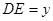 ,試求y關于x的函數解析式;
,試求y關于x的函數解析式;
(3)當 為多少時,以Q、D、E為頂點的三角形與
為多少時,以Q、D、E為頂點的三角形與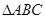 相似.
相似.
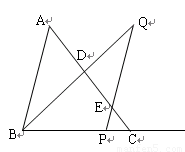
解:(1)聯結AQ
∵AB∥PQ AB=PQ
∴AQ∥BP AQ=BP
∵BP=3
∴AQ=3
∵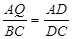
∴
∴
(2) ∵AB∥PQ,AQ∥BC
∴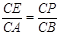 ,
,
∵ ,
, ,
, ,
, ,
,
當點P在邊BC上時,
∴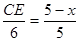 , 解得
, 解得
 , 解得
, 解得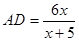
∴ 
當點P在邊BC的延長線上時,

∴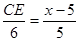 , 解得
, 解得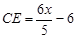
 , 解得
, 解得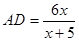
∴ 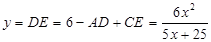
綜上, (
( )
)
(3)∵AB∥PQ,∴△EDQ∽△ADB
又以Q、D、E為頂點的三角形與 相似,
相似,
∴△ADB與 相似
相似
∵∠BAC公共,又∠ABD≠∠ABC
∴ ∠ABD=∠ACB
∴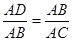 即
即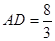
由(2)知,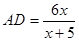
∴  得
得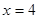
所以,當 為4時,以Q、D、E為頂點的三角形與
為4時,以Q、D、E為頂點的三角形與 相似.
相似.
【解析】(1)連接AQ,由平行四邊形的判定定理可得出四邊形ABPQ是平行四邊形,進而可得出△ADQ∽△CDB,由相似三角形的對應邊成比例即可得出結論;
(2)由平行線分線段成比例定理可知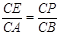 ,
, ,再根據點P在邊BC上或點P在邊BC的延長線上兩種情況討論即可;
,再根據點P在邊BC上或點P在邊BC的延長線上兩種情況討論即可;
(3)先由相似三角形的判定定理得出△EDQ∽△ADB,△ADB∽△ABC,由相似三角形的對應邊成比例即可求出BP的長.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
 如圖,已知△ABC中,AB=AC=10cm,BC=8cm,點D為AB的中點.
如圖,已知△ABC中,AB=AC=10cm,BC=8cm,點D為AB的中點.查看答案和解析>>
科目:初中數學 來源: 題型:
 34、如圖,已知△ABC中,AB=AC,AB的垂直平分線交AB于D,交AC于E,若△ABC與△EBC的周長分別是26cm、18cm,則AC=
34、如圖,已知△ABC中,AB=AC,AB的垂直平分線交AB于D,交AC于E,若△ABC與△EBC的周長分別是26cm、18cm,則AC=查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,已知△ABC中,AD=DB,D、E分別為BC、AB上一點,連接DE,∠1=∠2.
如圖,已知△ABC中,AD=DB,D、E分別為BC、AB上一點,連接DE,∠1=∠2.查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,已知△ABC中,AB>AC,BE、CF都是△ABC的高,P是BE上一點且BP=AC,Q是CF延長線上一點且CQ=AB,連接AP、AQ、QP,求證:
如圖,已知△ABC中,AB>AC,BE、CF都是△ABC的高,P是BE上一點且BP=AC,Q是CF延長線上一點且CQ=AB,連接AP、AQ、QP,求證:查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com