
 如圖,在Rt△ABC中,∠B=90°,AC=10cm,BC=6cm,現有兩個動點P,Q分別從點A和點B同時出發,其中點P以每秒2cm的速度沿AB向終點B移動,點Q以每秒1cm的速度沿BC向終點C移動,其中一點到終點,另一點也隨之停止.連接PQ.設動點運動時間是x秒.
如圖,在Rt△ABC中,∠B=90°,AC=10cm,BC=6cm,現有兩個動點P,Q分別從點A和點B同時出發,其中點P以每秒2cm的速度沿AB向終點B移動,點Q以每秒1cm的速度沿BC向終點C移動,其中一點到終點,另一點也隨之停止.連接PQ.設動點運動時間是x秒.分析 (1)首先運用勾股定理求出AB邊的長度,然后根據路程=速度×時間,分別表示出BQ、PB的長度;
(2)由于∠B=90°,如果△PBQ為等腰三角形,那么只有一種情況,即BP=BQ,由(1)的結果,可列出方程,從而求出x的值;
(3)根據四邊形APQC的面積=△ABC的面積-△PBQ的面積,列出方程,根據解的情況即可判斷.
解答 解:(1)∵∠B=90°,AC=10,BC=6,
∴AB=8.
∴BQ=x,PB=8-2x;
(2)由題意,得
8-2x=x,
∴x=$\frac{8}{3}$.
∴當x=$\frac{8}{3}$時,△PBQ為等腰三角形;
(3)假設存在x的值,使得四邊形APQC的面積等于20cm2,
則 $\frac{1}{2}$×6×8-$\frac{1}{2}$x(8-2x)=20,
解得x1=x2=2.
∴假設成立,所以當x=2時,四邊形APQC面積的面積等于20cm2.
點評 本題考查了三角形綜合題、動點問題、勾股定理,路程與速度、時間的關系,等腰三角形的性質以及不規則圖形的面積計算,綜合性較強,解題的關鍵是用方程的思想解決問題,屬于中考常考題型.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 科目 | 語文 | 數學 | 英語 |
| 得分 | 120 | 146 | 140 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
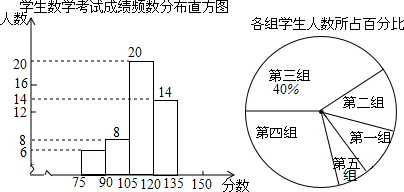
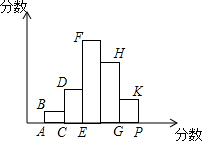 如圖所示,根據某班54個學生的數學成績繪制的頻數分布直方圖中,各小長方形的高的比AB:CD:EF:GH:PK=1:3:7:5:2,若后兩組為80分以上學生數,則80分以上學生人數是21.
如圖所示,根據某班54個學生的數學成績繪制的頻數分布直方圖中,各小長方形的高的比AB:CD:EF:GH:PK=1:3:7:5:2,若后兩組為80分以上學生數,則80分以上學生人數是21.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com