Question

9．如圖1，梯形ABCD中，AD∥BC，AB=AD=DC=5，BC=11．一個動點P從點B出發(fā)，以每秒1個單位長度的速度沿線段BC方向運動，過點P作PQ⊥BC，交折線段BA-AD于點Q，以PQ為邊向右作正方形PQMN，點N在射線BC上，當(dāng)Q點到達(dá)D點時，運動結(jié)束．設(shè)點P的運動時間為t秒（t＞0）．
（1）當(dāng)正方形PQMN的邊MN恰好經(jīng)過點D時，求運動時間t的值；
（2）如圖2，當(dāng)點Q在線段AD上運動時，線段PQ與對角線BD交于點E，將△DEQ沿BD翻折，得到△DEF，連接PF．是否存在這樣的t，使△PEF是等腰三角形？若存在，求出對應(yīng)的t的值；若不存在，請說明理由．

Answer 1

分析 （1）作AG⊥BC，DH⊥BC，垂足分別為G、H，可以得出四邊形AGHD為矩形，根據(jù)矩形的性質(zhì)及相關(guān)條件可以得出△ABG≌△DCH，可以求出BG=CH的值，再由勾股定理就可以求出AG=DH的值，就可以求出BP的值，即可以求出結(jié)論t的值；
（2）先由條件可以求出EF=EQ=PQ-EP=4-$\frac{1}{2}$t，分為三種情況：EF=EP時可以求出t值；當(dāng)FE=FP時，作FR⊥EP，垂足為R，可以求出t值；當(dāng)PE=PF時，作PS⊥EF，垂足為S，可以求出t值；即可得出結(jié)果．

解答 解：（1）如圖2，作AG⊥BC，DH⊥BC，垂足分別為G、H，
∴四邊形AGHD為矩形．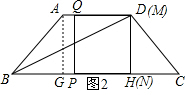
∵梯形ABCD，AB=AD=DC=5，
∴△ABG≌△DCH，
∴BG=$\frac{1}{2}$（BC-AD）=3，AG=4，
∴當(dāng)正方形PQMN的邊MN恰好經(jīng)過點D時，點M與點D重合，此時MQ=4，
∴GP=AQ=AD-DQ=1，BP=BG+GP=4，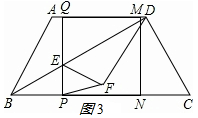
∴t=4，
即4秒時，正方形PQMN的邊MN恰好經(jīng)過點D；
（2）∵∠PEF+∠QEF=180°=∠QDF+∠QEF，
∴∠PEF=∠QDF=2∠ADB=∠ABC，
∴cos∠ABC=cos∠PEF=$\frac{3}{5}$，
由（1）可知EP=$\frac{1}{2}$BP=$\frac{1}{2}$t，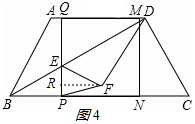
則EF=EQ=PQ-EP=4-$\frac{1}{2}$t，
①如圖3，當(dāng)EF=EP時，4-$\frac{1}{2}$t=$\frac{1}{2}$t，
∴t=4；
②如圖4，當(dāng)FE=FP時，作FR⊥EP，垂足為R，
∴ER=$\frac{1}{2}$EP=$\frac{3}{5}$EF，
∴$\frac{1}{2}$×$\frac{1}{2}$t=$\frac{3}{5}$（4-$\frac{1}{2}$t），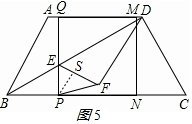
∴t=$\frac{48}{11}$；
③如圖5，當(dāng)PE=PF時，作PS⊥EF，垂足為S，
∵ES=$\frac{1}{2}$EF=$\frac{3}{5}$PE，
∴$\frac{1}{2}$（4-$\frac{1}{2}$t）=$\frac{3}{5}$×$\frac{1}{2}$t，
∴t=$\frac{40}{11}$．
∴當(dāng)t=4或$\frac{48}{11}$或$\frac{40}{11}$時，△PEF是等腰三角形．

點評 本題是四邊形綜合題目，考查了動點問題的運用，等腰直角梯形的性質(zhì)的運用，全等三角形的判定及性質(zhì)，等腰三角形的性質(zhì)等知識；本題綜合性強，有一定難度，特別是（2）中需要進(jìn)行分類討論才能得出結(jié)果．