
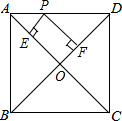
 如圖,在正方形ABCD中,AB=1,P是線段AD上的動點,PE⊥AC于點E,PF⊥BD于點F,則PE+PF的值為 ( )
如圖,在正方形ABCD中,AB=1,P是線段AD上的動點,PE⊥AC于點E,PF⊥BD于點F,則PE+PF的值為 ( )| A. | $\sqrt{2}$ | B. | 4 | C. | 2 | D. | $\frac{{\sqrt{2}}}{2}$ |
分析 根據正方形的對角線互相垂直可得OA⊥OD,對角線平分一組對角可得∠OAD=45°,然后求出四邊形OEPF為矩形,△AEP是等腰直角三角形,再根據矩形的對邊相等可得PF=OE,根據等腰直角三角形的性質可得PE=OE,從而得到PE+PF=OA,然后根據正方形的性質解答即可.
解答 解:在正方形ABCD中,OA⊥OB,∠OAD=45°,
∵PE⊥AC,PF⊥BD,
∴四邊形OEPF為矩形,△AEP是等腰直角三角形,
∴PF=OE,PE=AE,
∴PE+PF=AE+OE=OA,
∵正方形ABCD的邊長為1,
∴OA=$\frac{1}{2}$AC=$\frac{1}{2}$×$\sqrt{{1}^{2}+{1}^{2}}$=$\frac{\sqrt{2}}{2}$.
故選D.
點評 本題考查了正方形的性質,矩形的判定與性質,等腰直角三角形的判定與性質,熟記各性質求出PE+PF=OA是解題的關鍵.


科目:初中數學 來源: 題型:解答題
 LED燈具有環保節能、投射范圍大、無頻閃、使用壽命較長等特點,在日常生活中,人們更傾向于LED燈的使用,某校數學興趣小組為了解LED燈泡與普通白熾燈泡的銷售情況,進行了市場調查:某商場購進一批30瓦的LED燈泡和普通白熾燈泡進行銷售,其進價與標價如下表:
LED燈具有環保節能、投射范圍大、無頻閃、使用壽命較長等特點,在日常生活中,人們更傾向于LED燈的使用,某校數學興趣小組為了解LED燈泡與普通白熾燈泡的銷售情況,進行了市場調查:某商場購進一批30瓦的LED燈泡和普通白熾燈泡進行銷售,其進價與標價如下表:| LED燈泡 | 普通白熾燈泡 | |
| 進價(元) | 45 | 25 |
| 標價(元) | 60 | 30 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | a>b>c | B. | c>a>b | C. | c>b>a | D. | a>c>b |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{3}{5}$ | B. | $\frac{5}{9}$ | C. | $\frac{4}{9}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 三角形的中線、角平分線,高線都是線段 | |
| B. | 有一個內角是直角的三角形是直角三角形 | |
| C. | 任意三角形的外角和都是360° | |
| D. | 三角形的一個外角大于任何一個內角 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com