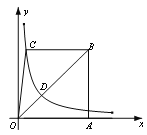
【題目】如圖，已知梯形ABCO的底邊AO在
軸上，
，AB⊥AO，過點C的雙曲線
交OB于D，且
，若△OBC的面積等于3，則k的值為__________．
【答案】
【解析】
設C（x，y），BC=a．過D點作DE⊥OA于E點．根據DE∥AB得比例線段表示點D坐標；根據△OBC的面積等于3得關系式，列方程組求解．
設C（x，y），BC=a．
則AB=y，OA=x+a．
過D點作DE⊥OA于E點．
∵OD：DB=1：2，DE∥AB，
∴△ODE∽△OBA，相似比為OD：OB=1：3，
∴DE=
AB=y，OE=OA=（x+a）．
∵D點在反比例函數的圖象上，且D（（x+a），y），
∴y（x+a）=k，即xy+ya=9k，
∵C點在反比例函數的圖象上，則xy=k，
∴ya=8k．
∵△OBC的面積等于3，
∴
ya=3，即ya=6．
∴8k=6，k=．
故答案為：．
永乾教育寒假作業快樂假期延邊人民出版社系列答案科目：初中數學 來源： 題型：
【題目】求證：相似三角形對應角的角平分線之比等于相似比．
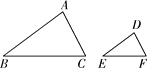
要求：①分別在給出的相似三角形△ABC與△DEF中用尺規作出一組對應角的平分線，不寫作法，保留作圖痕跡；
②在完成作圖的基礎上，寫出已知、求證，并加以證明．
查看答案和解析>>
科目：初中數學 來源： 題型：
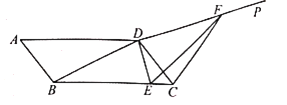
【題目】如圖，在
中，
，對角線
，點E是線段BC上的動點，連接DE，過點D作DP⊥DE，在射線DP上取點F，使得
，連接CF,則
周長的最小值為___________.
查看答案和解析>>
科目：初中數學 來源： 題型：
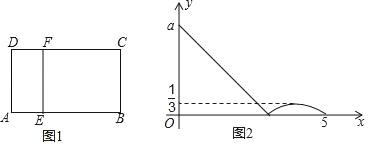
【題目】如圖1，在矩形ABCD中，動點E從A出發，沿A→B→C方向運動，當點E到達點C時停止運動，過點E作EF⊥AE交CD于點F，設點E運動路程為x，CF=y，如圖2所表示的是y與x的函數關系的大致圖象，給出下列結論：①a=3；②當CF=
時，點E的運動路程為
或
或
，則下列判斷正確的是（ ）
A. ①②都對 B. ①②都錯 C. ①對②錯 D. ①錯②對
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知矩形ABCD和矩形EFGO在平面直角坐標系中，點B，F的坐標分別為(－4,4)，(2,1)．若矩形ABCD和矩形EFGO是位似圖形，點P(點P在GC上)是位似中心，則點P的坐標為( )
A. (0,3)
B. (0,2.5)
C. (0,2)
D. (0,1.5)
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系xOy中，矩形OABC的頂點A在x軸的正半軸上，頂點C在y軸的正半軸上，D是BC邊上的一點，OC：CD＝5：3，DB＝6．反比例函數y＝
（k≠0）在第一象限內的圖象經過點D，交AB于點E，AE：BE＝1：2．
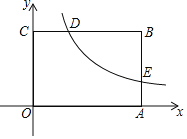
（1）求這個反比例函數的表達式；
（2）動點P在矩形OABC內，且滿足S△PAO＝
S四邊形OABC．
①若點P在這個反比例函數的圖象上，求點P的坐標；
②若點Q是平面內一點使得以A、B、P、Q為頂點的四邊形是菱形求點Q的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀下列材料，關于x的方程：x+
＝c+
的解是x1＝c，x2＝；x﹣＝c﹣的解是x1＝c，x2＝﹣；x+
＝c+
的解是x1＝c，x2＝；x+
＝c+
的解是x1＝c，x2＝；……
（1）請觀察上述方程與解的特征，比較關于x的方程x+
＝c+
（a≠0）與它們的關系猜想它的解是什么，并利用“方程的解”的概念進行驗證．
（2）可以直接利用（1）的結論，解關于x的方程：x+
＝a+
．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1，DE是⊙O的直徑，點A、C是直徑DE上方半圓上的兩點，且AO⊥CO．連接AE，CD相交于點F，點B是直徑DE下方半圓上的任意一點，連接AB交CD于點G，連接CB交AE于點H．
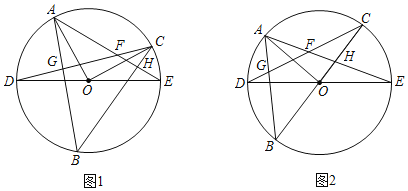
（1）∠ABC＝ ；
（2）證明：△CFH∽△CBG；
（3）若弧DB為半圓的三分之一，把∠AOC繞著點O旋轉，使點C、O、B在一直線上時，如圖2，求
的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
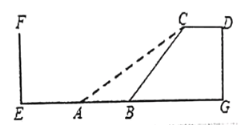
【題目】速滑運動受到許多年輕人的喜愛。如圖，四邊形
是某速滑場館建造的滑臺，已知
，滑臺的高
為
米，且坡面
的坡度為
.后來為了提高安全性，決定降低坡度，改造后的新坡面AC的坡度為
.
（1）求新坡面
的坡角及的長；
（2）原坡面底部
的正前方
米處
是護墻
，為保證安全，體育管理部門規定，坡面底部至少距護墻
米。請問新的設計方案能否通過，試說明理由（參考數據：
）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com