
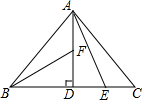
 如圖,在Rt△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足為D.E、F分別是CD、AD上的點,且CE=AF.若∠AED=62°,則∠DBF=28度.
如圖,在Rt△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足為D.E、F分別是CD、AD上的點,且CE=AF.若∠AED=62°,則∠DBF=28度. 分析 利用等腰三角形的三線合一,直角三角形的性質,可得BD=AD=CD,根據斜邊和直角邊對應相等可以證明△BDF≌△ADE,利用角的關系即可求得∠DBF的度數.
解答 解:∵AB=AC,AD⊥BC,
∴BD=CD,
又∵∠BAC=90°,
∴BD=AD=CD,
又∵CE=AF,
∴DF=DE,
在△BDF與△ADE中,$\left\{\begin{array}{l}{BD=AD}\\{∠BDF=∠ADE}\\{DF=DE}\end{array}\right.$,
∴△BDF≌△ADE(SAS).
∴∠DBF=∠DAE=90°-∠AED=90°-62°=28°.
故答案為:28.
點評 本題主要考查了全等三角形的判定與性質,解題的關鍵是熟練運用等腰直角三角形三線合一性質、直角三角形斜邊上的中線等于斜邊的一半.


科目:初中數學 來源: 題型:選擇題
| A. | $\sqrt{4}$ | B. | $\sqrt{8}$ | C. | $\sqrt{10}$ | D. | $\sqrt{12}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 某氣象研究中心觀測一場沙塵暴從發生到結束全過程,開始時風暴平均每小時增加2千米/時,2小時后,沙塵暴經過開闊荒漠地,風速變為平均每小時增加4千米/時,一段時間,風暴保持不變,當沙塵暴遇到綠色植被區時,其風速平均每小時減小1千米/時,最終停止.結合風速y千米/小時與時間x(小時)的圖象,回答下列問題:
某氣象研究中心觀測一場沙塵暴從發生到結束全過程,開始時風暴平均每小時增加2千米/時,2小時后,沙塵暴經過開闊荒漠地,風速變為平均每小時增加4千米/時,一段時間,風暴保持不變,當沙塵暴遇到綠色植被區時,其風速平均每小時減小1千米/時,最終停止.結合風速y千米/小時與時間x(小時)的圖象,回答下列問題:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
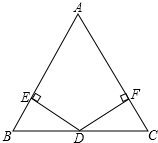 如圖,已知△ABC中,AB=AC,點D是BC的中點,DE⊥AB于點E,DF⊥AC于點F,請你用不同的方法證明:DE=DF.(用到相同的知識點即視為同一種方法)
如圖,已知△ABC中,AB=AC,點D是BC的中點,DE⊥AB于點E,DF⊥AC于點F,請你用不同的方法證明:DE=DF.(用到相同的知識點即視為同一種方法)查看答案和解析>>
科目:初中數學 來源: 題型:填空題
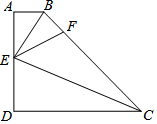 如圖,在四邊形ABCD中,AB∥CD,∠D=90°,E為AD上一點,分別以EB,EC為折痕將這兩個角(∠A,∠D)向內折起,點A,D恰好落在BC邊的F處,若AB=1,DC=4,則△EBC的面積為5.
如圖,在四邊形ABCD中,AB∥CD,∠D=90°,E為AD上一點,分別以EB,EC為折痕將這兩個角(∠A,∠D)向內折起,點A,D恰好落在BC邊的F處,若AB=1,DC=4,則△EBC的面積為5.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com