
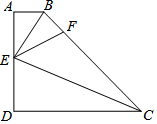
 如圖,在四邊形ABCD中,AB∥CD,∠D=90°,E為AD上一點,分別以EB,EC為折痕將這兩個角(∠A,∠D)向內折起,點A,D恰好落在BC邊的F處,若AB=1,DC=4,則△EBC的面積為5.
如圖,在四邊形ABCD中,AB∥CD,∠D=90°,E為AD上一點,分別以EB,EC為折痕將這兩個角(∠A,∠D)向內折起,點A,D恰好落在BC邊的F處,若AB=1,DC=4,則△EBC的面積為5. 分析 作BH⊥CD于H,根據翻轉變換的性質得到,BF=AB=1,CF=CD=4,△AEB≌△FEB,△DEC≌△FEC,根據勾股定理求出BH,求出梯形ABCD的面積,得到答案.
解答 解:作BH⊥CD于H,
由翻轉變換的性質可知,BF=AB=1,CF=CD=4,△AEB≌△FEB,△DEC≌△FEC,
∴BC=BF+CF=5,CH=CD-DH=3,
∴BH=$\sqrt{B{C}^{2}-C{H}^{2}}$=4,
∴梯形ABCD的面積=$\frac{1}{2}$×(AB+CD)×AD=10,
∴△EBC的面積=$\frac{1}{2}$×梯形ABCD的面積=5,
故答案為:5.
點評 本題考查了折疊的性質:折疊是一種對稱變換,它屬于軸對稱,折疊前后圖形的形狀和大小不變,位置變化,對應邊和對應角相等.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
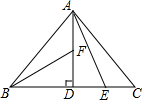 如圖,在Rt△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足為D.E、F分別是CD、AD上的點,且CE=AF.若∠AED=62°,則∠DBF=28度.
如圖,在Rt△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足為D.E、F分別是CD、AD上的點,且CE=AF.若∠AED=62°,則∠DBF=28度.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
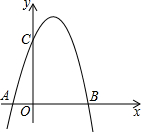 如圖,對稱軸為直線x=$\frac{1}{2}$的拋物線經過B(2,0),C(0,4)兩點,拋物線與x軸的另一交點為A.
如圖,對稱軸為直線x=$\frac{1}{2}$的拋物線經過B(2,0),C(0,4)兩點,拋物線與x軸的另一交點為A.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 了解2017年報考飛行員的學生的視力情況應采取抽樣調查 | |
| B. | 打開電視機,正在播放“神奇的動物去哪里”制作花絮是必然事件 | |
| C. | 為了初三1200名學生的體能狀況,從中抽取了100名學生的成績進行分析,1200是樣本容量 | |
| D. | 7,9,9,4,9,8,8,這組數據的眾數是9 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | a>-1 | B. | -1≤a<0 | C. | -1<a≤0 | D. | a≤0 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 4π | B. | $\frac{4}{3}π$ | C. | $\frac{2}{3}π$ | D. | $\frac{16}{3}π$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com