
【題目】如圖1,在平面直角坐標系中點![]() ,
,![]() ,以
,以![]() 為頂點在第一象限內(nèi)作正方形
為頂點在第一象限內(nèi)作正方形![]() .反比例函數(shù)
.反比例函數(shù)![]() 、
、![]() 分別經(jīng)過
分別經(jīng)過![]() 、
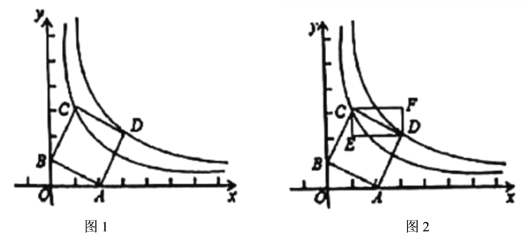
、![]() 兩點(1)如圖2,過
兩點(1)如圖2,過![]() 、
、![]() 兩點分別作
兩點分別作![]() 、
、![]() 軸的平行線得矩形
軸的平行線得矩形![]() ,現(xiàn)將點
,現(xiàn)將點![]() 沿
沿![]() 的圖象向右運動,矩形
的圖象向右運動,矩形![]() 隨之平移;
隨之平移;
①試求當點![]() 落在
落在![]() 的圖象上時點
的圖象上時點![]() 的坐標_____________.
的坐標_____________.
②設(shè)平移后點![]() 的橫坐標為
的橫坐標為![]() ,矩形的邊
,矩形的邊![]() 與
與![]() ,
,![]() 的圖象均無公共點,請直接寫出
的圖象均無公共點,請直接寫出![]() 的取值范圍____________.
的取值范圍____________.
【答案】![]()
![]()
【解析】
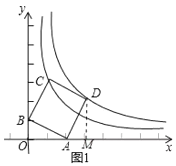
(1)如圖1中,作DM⊥x軸于M.利用全等三角形的性質(zhì)求出點D坐標,點C坐標,得到k1 ,k2的值,設(shè)平移后點D坐標為(m,![]() ),則E(m2,
),則E(m2,![]() ),由題意:(m2)
),由題意:(m2)![]() =3,解方程即可;
=3,解方程即可;
(2)設(shè)平移后點D坐標為(a,![]() ),則C(a2,
),則C(a2,![]() +1),當點C在y=
+1),當點C在y=![]() 上時,(a2)(
上時,(a2)(![]() +1)=6,解得a=1+
+1)=6,解得a=1+![]() 或1
或1![]() (舍棄),觀察圖象可得結(jié)論;
(舍棄),觀察圖象可得結(jié)論;
解:(1)如圖1中,作DM⊥x軸于M.
∵四邊形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∵∠AOB=∠AMD=90°,
∴∠OAB+∠OBA=90°,∠OAB+∠DAM=90°,
∴∠ABO=∠DAM,
∴△OAB≌△MDA(AAS),
∴AM=OB=1,DM=OA=2,
∴D(3,2),
∵點D在![]() 上,
上,
∴k2=6,即![]() ,
,
同法可得C(1,3),
∵點C在![]() 上,
上,
∴k1=3,即![]() ,
,
設(shè)平移后點D坐標為(m,![]() ),則E(m2,
),則E(m2,![]() ),
),
由題意:(m2)![]() =3,
=3,
解得m=4,
∴D(4,![]() );
);
(2)設(shè)平移后點D坐標為(a,![]() ),則C(a2,
),則C(a2,![]() +1),
+1),
當點C在y=![]() 上時,(a2)(
上時,(a2)(![]() +1)=6,
+1)=6,
解得a=1+![]() 或1
或1![]() (舍棄),
(舍棄),
觀察圖象可知:矩形的邊CE與![]() ,
,![]() 的圖象均無公共點,
的圖象均無公共點,
則a的取值范圍為:4<a<1+![]() .
.


 期末好成績系列答案
期末好成績系列答案 99加1領(lǐng)先期末特訓卷系列答案
99加1領(lǐng)先期末特訓卷系列答案 百強名校期末沖刺100分系列答案
百強名校期末沖刺100分系列答案 好成績1加1期末沖刺100分系列答案
好成績1加1期末沖刺100分系列答案 金狀元績優(yōu)好卷系列答案
金狀元績優(yōu)好卷系列答案科目:初中數(shù)學 來源: 題型:
【題目】為了解2018年某校九年級數(shù)學質(zhì)量監(jiān)控情況,隨機抽取40名學生的數(shù)學成績進行分析.
成績統(tǒng)計如下.
93 | 92 | 84 | 55 | 85 | 82 | 66 | 75 | 88 | 67 |
87 | 87 | 37 | 61 | 86 | 61 | 77 | 57 | 72 | 75 |
68 | 66 | 79 | 92 | 86 | 87 | 61 | 86 | 90 | 83 |
90 | 18 | 70 | 67 | 52 | 79 | 86 | 71 | 61 | 89 |
2018年某校九年級數(shù)學質(zhì)量監(jiān)控部分學生成績統(tǒng)計表:
分數(shù)段 | x<50 | 50≤x<60 | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x<100 |
人數(shù) | 2 | 3 | 9 | 13 |
平均數(shù)、中位數(shù)、眾數(shù)如下表:
統(tǒng)計量 | 平均數(shù) | 中位數(shù) | 眾數(shù) |
分值 | 74.2 | 78 | 86 |
請根據(jù)所給信息,解答下列問題:
(1)補全統(tǒng)計表中的數(shù)據(jù);
(2)用統(tǒng)計圖將2018年某校九年級數(shù)學質(zhì)量監(jiān)控部分學生成績表示出來;
(3)根據(jù)以上信息,提出合理的復(fù)習建議.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,Rt△OAB的頂點O與坐標原點重合,∠AOB=90°,AO=2BO,當點A在反比例函數(shù)![]() (x>0)的圖像上移動時,點B的坐標滿足的函數(shù)表達式為( )
(x>0)的圖像上移動時,點B的坐標滿足的函數(shù)表達式為( )

A. ![]() (x<0) B.
(x<0) B. ![]() (x<0)
(x<0)
C. ![]() (x<0) D.
(x<0) D. ![]() (x<0)
(x<0)
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
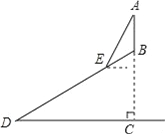
【題目】如圖,某班數(shù)學興趣小組利用數(shù)學活動課時間測量位于山頂?shù)碾娨曀嗀B的高度,已知山的坡度為30°,山高857.5尺,組員從山腳D處沿山坡向著電視塔方向前進1620尺到達E點,在點E處測得電視塔頂端A的仰角為60°,求電視塔AB的高度.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
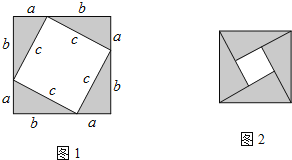
【題目】閱讀下面的材料:勾股定理神秘而美妙,它的證法多種多樣,下面是教材中介紹的一種拼圖證明勾股定理的方法.先做四個全等的直角三角形,設(shè)它們的兩條直角邊分別為a,b,斜邊為c,然后按圖1的方法將它們擺成正方形.
由圖1可以得到(a+b)2=4×![]() ab+c2
ab+c2
整理,得a2+2ab+b2=2ab+c2.
所以a2+b2=c2.
如果把圖1中的四個全等的直角三角形擺成圖2所示的正方形,請你參照上述方法證明勾股定理.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】定義:如圖(1),![]() ,
,![]() ,
,![]() ,
,![]() 四點分別在四邊形
四點分別在四邊形![]() 的四條邊上,若四邊形
的四條邊上,若四邊形![]() 為菱形,我們稱菱形
為菱形,我們稱菱形![]() 為四邊形
為四邊形![]() 的內(nèi)接菱形.
的內(nèi)接菱形.
動手操作:

(1)如圖2,網(wǎng)格中的每個小四邊形都為正方形,每個小四邊形的頂點叫做格點,由![]() 個小正方形組成一個大正方形
個小正方形組成一個大正方形![]() ,點
,點![]() 、
、![]() 在格點上,請在圖(2)中畫出四邊形
在格點上,請在圖(2)中畫出四邊形![]() 的內(nèi)接菱形
的內(nèi)接菱形![]() ;
;
特例探索:
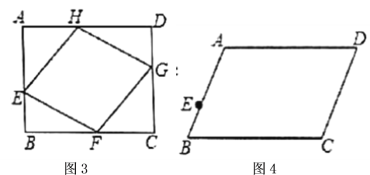
(2)如圖3,矩形![]() ,
,![]() ,點
,點![]() 在線段
在線段![]() 上且
上且![]() ,四邊形
,四邊形![]() 是矩形
是矩形![]() 的內(nèi)接菱形,求
的內(nèi)接菱形,求![]() 的長度;
的長度;
拓展應(yīng)用:
(3)如圖4,平行四邊形![]() ,
,![]() ,
,![]() ,點
,點![]() 在線段
在線段![]() 上且
上且![]() ,
,
①請你在圖4中畫出平行四邊形![]() 的內(nèi)接菱形
的內(nèi)接菱形![]() ,點
,點![]() 在邊
在邊![]() 上;
上;
②在①的條件下,當![]() 的長最短時,
的長最短時,![]() 的長為__________
的長為__________
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】以下是兩張不同類型火車的車票:(“D×××次”表示動車,“G×××次”表示高鐵):
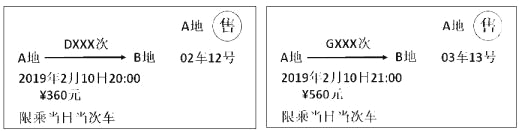
(1)根據(jù)車票中的信息填空:兩車行駛方向 ,出發(fā)時刻 (填“相同”或“不同”);
(2)已知該動車和高鐵的平均速度分別為200km/h,300km/h,如果兩車均按車票信息準時出發(fā),且同時到達終點,求A,B兩地之間的距離;
(3)在(2)的條件下,請求出在什么時刻兩車相距100km?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】已知![]() 三點在數(shù)軸上所對應(yīng)的數(shù)分別為
三點在數(shù)軸上所對應(yīng)的數(shù)分別為![]() 且
且![]() 滿足
滿足![]() .動點
.動點![]() 從點
從點![]() 出發(fā),以2單位/秒的速度向右運動,同時,動點
出發(fā),以2單位/秒的速度向右運動,同時,動點![]() 從點
從點![]() 出發(fā),以1單位秒的速度向左運動,線段
出發(fā),以1單位秒的速度向左運動,線段![]() 為“變速區(qū)”,規(guī)則為: 從點
為“變速區(qū)”,規(guī)則為: 從點![]() 運動到點
運動到點![]() 期間速度變?yōu)樵瓉淼囊话耄罅⒖袒謴?fù)原速,從點
期間速度變?yōu)樵瓉淼囊话耄罅⒖袒謴?fù)原速,從點![]() 運動到點
運動到點![]() 期間速度變?yōu)樵瓉淼膬杀叮笠擦⒖袒謴?fù)原速.當點
期間速度變?yōu)樵瓉淼膬杀叮笠擦⒖袒謴?fù)原速.當點![]() 到達點
到達點![]() 時,兩點都停止運動.設(shè)運動的時間為
時,兩點都停止運動.設(shè)運動的時間為![]() 秒.
秒.
(1) ![]() ______,
______,![]() ______,
______,![]() ______;
______;
(2)①動點![]() 從點
從點![]() 運動至點
運動至點![]() 時,求
時,求![]() 的值;
的值;
②![]() 兩點相遇時,求相遇點在數(shù)軸上所對應(yīng)的數(shù);
兩點相遇時,求相遇點在數(shù)軸上所對應(yīng)的數(shù);
(3)若點![]() 為線段
為線段![]() 中點,當
中點,當![]() ________秒時,
________秒時,![]() .
.
![]()
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com